Gravity in Diagrams

by James E. Anderson

Edited by the USITC Gravity Modeling Group

Introduction

The recent prominence of gravity in applied trade and trade policy analysis is obscured in fog of algebra when viewed by an audience with less than advanced economics training. A large segment of the trade policy making community thus has only a vague sense of the credibility of gravity exercises such as calculating the effect of NAFTA or Brexit. Reported numbers for changes in trade and real incomes of partners and third parties emerge from the computer simulations as from a black box. Opening the box and exposing the mechanism inside is the goal of this note. The workings of gravity are set in the demand and supply diagram of Economics 101. Supply and demand shifts are linked across countries by spatial arbitrage. Full understanding of the resulting linkages unavoidably requires algebra, but the diagram is a lens that pierces the mist.

Gravity and What-if Questions discusses why the gravity model is chosen in recent applied and academic work to supply answers to 'what if' trade policy questions often posed to the modeling community.

Supply and Demand Analysis sets out a supply and demand description of the gravity model and its mechanism. A key concept is economic incidence – the decomposition of trade costs into the portions borne by buyer and seller.

Comparative Statics describes how the mechanism works to answer 'what if' questions.

The Gravity Equation describes the gravity equation, first in its original 'noneconomic' form and then in its economic structural form.

Gravity and Arbitrage Equilibrium and General Equilibrium Simulations describe the mechanism that finds the equilibrium distribution of multiple sourced goods to multiple markets. Algebra is unavoidable here. For the many readers not comfortable with algebra, these sections should be approached for a sense of how the diagrammatic presentation can 'find' a new what-if equilibrium starting from the old one and imposing the hypothesized trade cost changes.

Gravity and Arbitrage Equilibrium explains how the gravity model – structure imposed on the gravity equation – finds an equilibrium distribution of goods that satisfies elementary economic adding-up requirements.

Multilateral and Bilateral Incidence extends the concept of incidence in one market of Supply and Demand Analysis to multi-market incidence, the key mechanism linking changes in some trade costs to their effects on all bilateral markets.

General Equilibrium Simulations concludes with a description of how the gravity model mechanism is used to calculate answers to what-if questions such as Brexit – big changes that affect multiple goods and multiple countries through gravity interaction. The exposition explains how the numerical methods used on computers find the answers to what if questions require this full general equilibrium treatment.

Gravity and What-if Questions

Analysts often use the estimated gravity model in counter-factual exercises that predict the effects of policy changes (what if NAFTA is destroyed or Brexit occurs), or to account for the effects of past policy changes (what did NAFTA do, all else equal). The goal of this paper is better understanding of how the gravity model produces counter-factual projections.

Begin thinking about counter-factual exercises with a partial equilibrium use of an estimated gravity model: calculate the effect of changing a tariff, part of the trade cost factor $t_{ij}$ that reduces shipments from origin $i$ to destination $j$. The estimated model predicts the elasticity of bilateral trade $X_{{ij}}$ with respect to $t_{ij}$. Estimated values of the trade elasticity range from 3 to 8 or higher depending on the sector to which the model is applied. Thus a 25% tariff (increased from 0) with a trade elasticity of 3 would reduce bilateral trade in percentage terms by 3 times the tariff increase, or a 75% fall.

Another example illustrates why the partial equilibrium counter-factual analysis often needs extension. Brexit implies that the UK would face the EU common tariff, averaging some 2.5%. A trade elasticity equal to 3 implies that UK exports (aggregate value across goods) to the EU would fall by some 7.5%. The EU received 44% of UK exports (in 2017) so this shift is significant. Where do the displaced goods go? Some would be sold in the UK and some to non-EU destinations. Prices of UK exports received by the sellers presumably will fall to absorb higher shipment costs to alternative foreign markets or to induce more domestic purchases in the UK. Brexiteers claim that the UK could negotiate trade agreements with other countries (more freely than via EU negotiations) to make up for the lost trade with the EU. Economist critics apply gravity to point out that the UK's non-EU customers are much further away than the EU. Some exports would naturally be diverted outside the EU, but they are so much more costly to serve that even with new trade agreements the added trade could not make up the 7.5% fall. (The UK average distance to North America is around 10 times its average distance to the EU. With a distance elasticity equal to $-1$, the relative distance effect reduces UK exports to North America relative to the EU by a factor of 10.)

To quantify the multi-market effects of Brexit, with or without new trade agreements, more elaborate counter-factual exercises based on the gravity model are required. Such exercises use the theory behind estimated gravity equations, the full gravity model that includes the equation. The black box is opened by analyzing bilateral trade with the partial equilibrium supply and demand diagram of the first course in economics (Economics 101).

Demand and Supply Analysis

Spatial Arbitrage

Supply and demand schedules describe the forces leading to equilibrium in any market. Spatial arbitrage across separated markets is the economic force linking the supply and demand schedules in any particular market. Gravity equation describes arbitrage equilibrium sales in any bilateral (country pair) market.

Autos are an example, produced by many countries and purchased from many countries. Economic agents allocate autos across destination markets to maximize profits. If the price paid for BMWs net of trade costs differs across destination countries there are arbitrage gains to be made by shifting autos from low net price to high net price destinations.

Arbitrageurs are the agents who reallocate planned goods sales across markets until no profit is to be made from further reallocation. In arbitrage equilibrium, sellers from $i$ receive net price $p_{i} = p_{{ij}}/t_{{ij}}$ from any destination $j$, hence $p_{{ij}} = p_{i}t_{{ij}}$ for any pair $i$ and $j$. Arbitrage permits a single supply and demand diagram to portray the connection of multiple markets, and in particular how changes in one bilateral trade cost $t_{{ij}}$ affect all bilateral markets, including bilateral pairs not involving either $i$ or $j$.

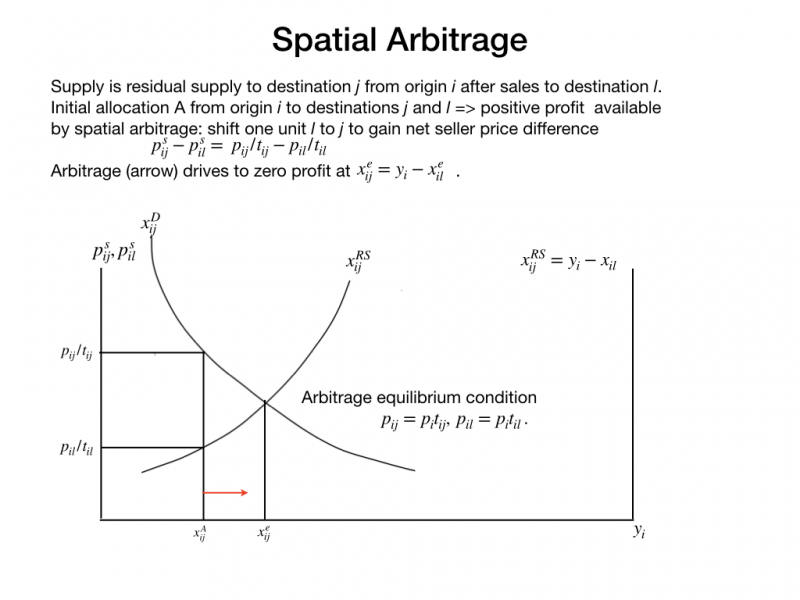
The review of supply and demand analysis begins with arbitrage illustrated in the figure above. Two markets, $j$ and $l$ receive sales from origin $i$. The vertical axis records net seller prices, buyer prices deflated by trade cost factors $p_{{ij}}^{s} = p_{{ij}}/t_{{ij}}$ and $p_{{il}}^{s} = p_{{il}}/t_{{il}}$. Demand in $j$ slopes downward because buyers substitute against increasingly expensive goods. Supply slopes upward because the same force is at work on the demand in $l$ that is deducted from supply to form residual supply. Thus supply to $j$ taken from $l$ comes at increasing opportunity cost. The initial allocation at $x_{{ij}}^{A}$ allows arbitrage profits: $p_{{ij}}^{s} - p_{{il}}^{s} > 0$ is the profit from shifting one unit from market $l$ to market $j$. Arbitrage equilibrium at $x_{{ij}}^{e}$ drives arbitrage profits to zero.¹

Gravity models of trade assume that spatial arbitrage is perfectly efficient to focus on the determinants of bilateral trade in a spatial arbitrage equilibrium. Focus on any single bilateral market with a supply and demand analysis thus has in the background the relationship of the focus market to all other markets in a world equilibrium system.

Incidence Review

The supply and demand diagram is next used to model economic incidence — the decomposition of trade costs into the portions borne by sellers and buyers — sellers' incidence and buyers' incidence respectively. Perfect spatial arbitrage is assumed here and henceforth.

Introductory economics derives the incidence analysis for a tax in a single isolated market, reviewed below. Incidence in the gravity model extends in a later section from a single bilateral market to overall incidence with the world for countries as buyers and sellers.

The figure below is the familiar (to Economics 101 students) supply and demand diagram describing equilibrium in a particular bilateral trade market for a particular type of good such as autos. A bilateral import demand schedule intersects with an export supply schedule representing the residual of total supply minus the aggregate of all other bilateral demands. Now origin $i$ serves many destinations, including (importantly) its own domestic market.

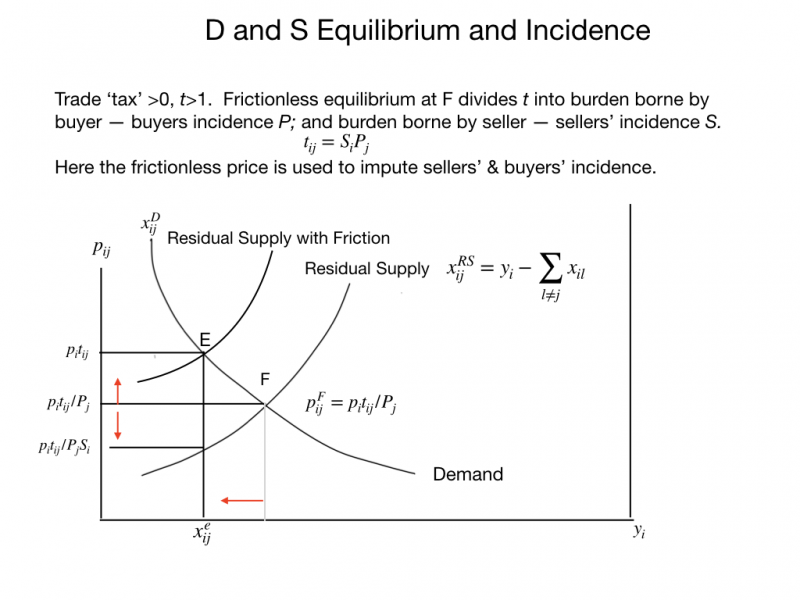
The left vertical axis in the figure above measures possible bilateral buyers' prices for goods from origin $i$ sold in destination $j$, $p_{{ij}}$. The right vertical axis is the aggregate supply of goods from seller $i$, assumed invariant to price. The horizontal axis measures possible bilateral trade volume on goods from $i$ in $j$. Demand is decreasing in price, demand schedule $x_{{ij}}^{D}$ slopes downward (as is confirmed by international trade empirical work). Supply schedule $x_{{ij}}^{{RS}}$ is a residual supply: total quantity $y_{i}$ minus the quantity sold from $i$ to all destinations (including the domestic one $x_{{ii}}$) except $j$. Residual supply slopes upward (is increasing in the cost of serving $j$) because shifting more sales to $j$ means taking sales away from other markets at increasing opportunity cost of the foregone sales to other markets. Opportunity cost rises because less sales in other markets raises their willingness to pay for the remaining goods, as reduced allocations drive them up their demand schedules. (In an alternative visual presentation, $x_{{ij}}^{{RS}}$ is also the aggregate demand for goods from $i$ by all destinations other than $j$, plotted with its origin at $y_{i}$ and its quantity rising moving to the left from $y_{i}$.) For now, treat $x_{{ij}}^{D},x_{{ij}}^{{RS}}$ as generic demand and supply schedules in partial equilibrium.

The figure depicts an equilibrium with a trade friction $t_{{ij}} > 1$ driving a wedge between the price paid by the buyer $p_{i}t_{{ij}}$ and the net price $p_{i}$ received by the seller. The hypothetical frictionless equilibrium is at point F. The trade friction shifts up the residual supply curve by the proportion $t_{{ij}}$ so that it intersects the demand curve $x_{{ij}}^{D}$ at $p_{i}t_{{ij}}$. The vertical line projected down from the intersection strikes residual supply schedule $x_{{ij}}^{{RS}}$ at seller price net of trade costs $p_{i}$.

The incidence of trade cost is read off the left hand vertical axis of the diagram. $p_{i}t_{{ij}}/P_{j}$ is equal to the frictionless equilibrium price $p_{{ij}}^{F}$. The friction (usually a tax in Economics 101) pushes the price the seller receives down from its frictionless level $p_{{ij}}^{F} = p_{i}t_{{ij}}/P_{j}$ to $p_{i}$. The buyers incidence of the trade cost is $P_{j}$. $S_{i} = (p_{i}t_{{ij}}/P_{j})/p_{i} = t_{{ij}}/P_{j}$ is the sellers' incidence of the trade cost. Then $S_{i}P_{i} = t_{{ij}}$, the actual friction is equivalent to the product of the sellers' incidence $S_{i}$ and the buyers' incidence $P_{i}$. The decomposition is based on the frictionless equilibrium price labeled $p_{{ij}}^{F} = p_{i}t_{{ij}}/P_{j}$. More usefully for present purposes, consider reducing $t_{{ij}}$ by actually dividing it by $S_{i}P_{j}$. The new buyers' and sellers' incidences are reduced to 1 and the equilibrium quantity is raised to $x_{{ij}}^{F}$.

Comparative Statics

A common exercise with estimated gravity models is to simulate the effect of a proposed change in trade costs, or to calculate an 'all else equal' evaluation of a historical change in trade costs. As an illustration of the latter, calculate the effect of NAFTA from a base year around its inception, hence controlling for other effects on trade that happened after NAFTA's inception. As for the former, calculate the effect of NAFTA changes from the current base.

The figure below illustrates the partial equilibrium comparative statics of a rise in $t_{{ij}}$. The rise in $t_{{ij}}$ at constant $p_{i}$ implies that sellers would be making a loss on sales of $x_{{ij}}^{0}$. Arbitrage shifts sales to other markets, raising the price paid in $j$ and lowering the prices paid in markets $l$ other than $j$. Eventually equilibrium is reached with equilibrium quantity $x_{{ij}}^{1}$ and buyers' price $p_{{ij}}^{1} = p_{i}^{1}t_{{ij}}^{1}$. Sellers receive $p_{i}^{1}t_{{ij}}^{1}/P_{j}^{1}S_{i}^{1}$.

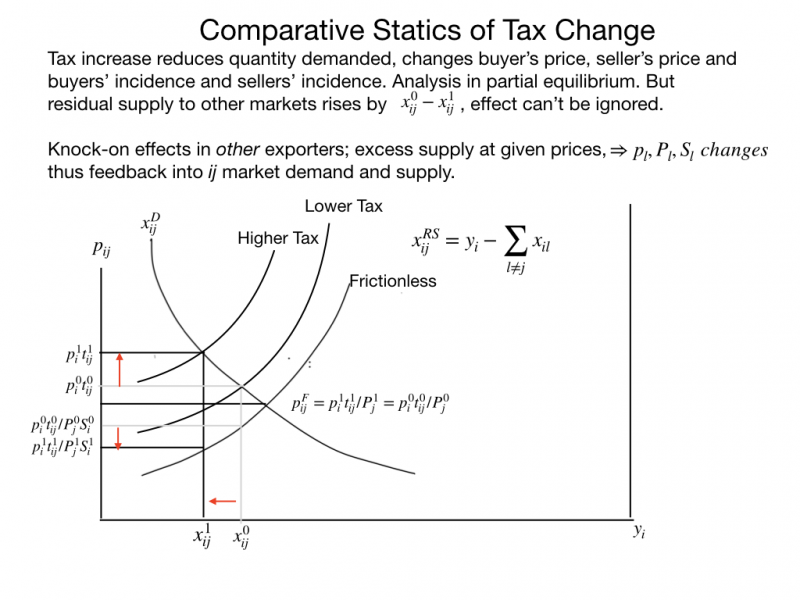
It would be an accident if the new partial equilibrium values for $p_{i}$, $S_{i}$ and $P_{j}$ on the figure were magically consistent with equilibrium in markets $l \neq j$. Quantity sold in market ${ij}$ falls by $x_{{ij}}^{0} - x_{{ij}}^{1}$. Thus residual supply to markets $l$ other than $j$ rises by this amount: $x_{il}^{{RS}}$ shifts to the right by $x_{{ij}}^{0} - x_{{ij}}^{1}$. Residual supply to markets other than $j$ is also affected by the change in seller $i$'s price $p_{i}$ and by seller and buyer incidences $S_{i}$ and $P_{j}$. Moreover, any shifts in equilibrium prices in other markets $lj$ would feed back to shift residual supply to market ${ij}$, $x_{{ij}}^{{RS}}$. The left vertical axis of the figure could be taken to record the magically consistent effects on market ${ij}$, but the values for $p_{i}^{1}$, $S_{i}^{1}$ and $P_{j}^{1}$ on the axis cannot be solved by a single shift in the tax-inclusive residual supply schedule moving along an invariant demand schedule.

The 'magic' requires finding new values for $p_{i}$, $S_{i}$ and $P_{j}$ consistent with equilibrium in all markets simultaneously. Further small shifts in demand and residual supply schedules in all markets are required for this. Nevertheless, the initial impacts of the tax change are appropriately illustrated in the figure above, as are valid ideas of what more shifting of supplies in spatial arbitrage must occur to find the new equilibrium.

Notice that the comparative statics analysis can be applied to illustrate effects in any bilateral trade market. With $N$ countries and $N$ goods, there are $N^{2}$ possible choices for the countries designated as origin $i$ and destination $j$. Each bilateral trade cost variation has effects on all other markets, even those not directly involving either $i$ or $j$. Usually more important would be effects on third parties involving either $i$ or $j$.

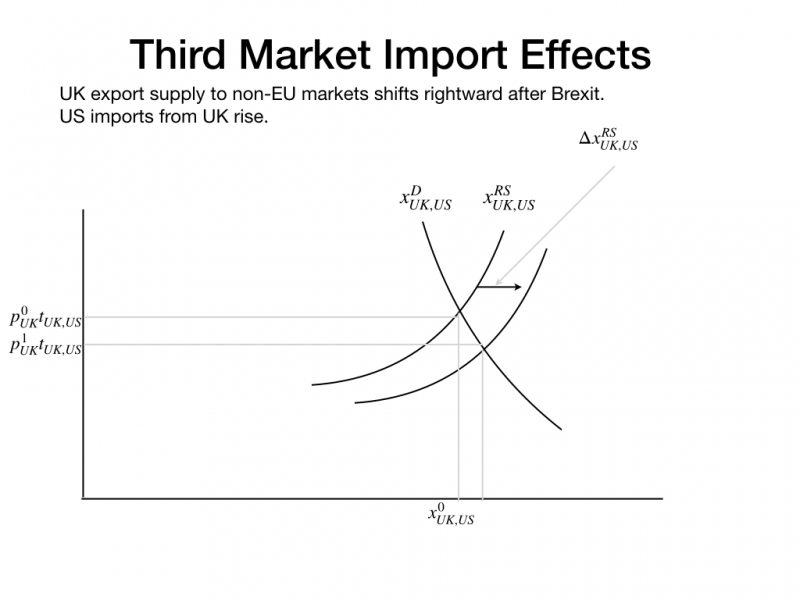
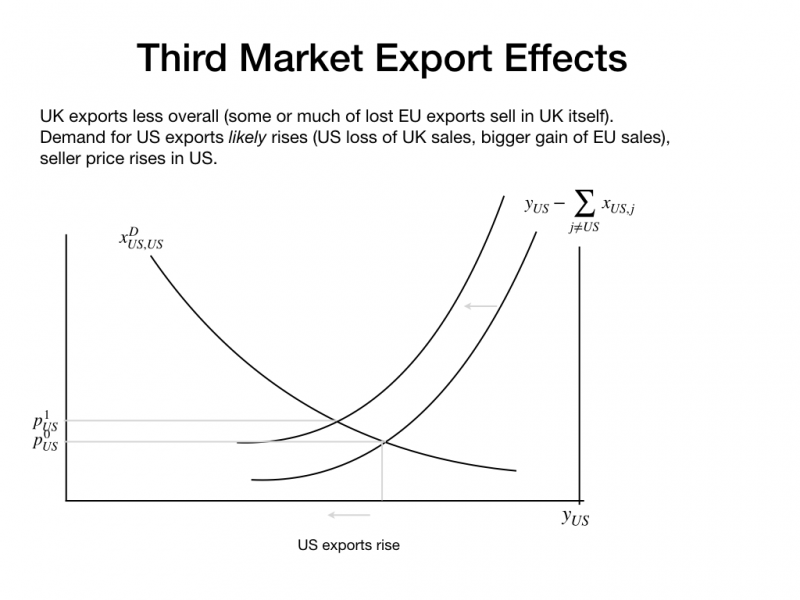
For example, consider the effect of Brexit on the US import and export trade with the UK. The next two diagrams portray the impact of Brexit with plausible guesses at the direction of the shifts in relevant demand and residual supply schedules. In the first figure below the US experiences a shift in residual supply from the UK, causing an increase in quantity demanded induced by a rise in sellers' incidence $S_{{UK}}$ and consequent fall in price of UK goods in the US. In the second figure below the US is likely to experience a rise in total exports because the sales lost to the UK (because UK domestic sales rise) are likely to be dominated by the gain in sales to the EU (because UK goods become more expensive to the EU).

A particular interest for trade policy analysis is the effect on domestic trade $x_{{jj}}$ of trade costs $t_{{ij}}$, particularly if the trade cost variation is uniform across suppliers $i \neq j$, as when MFN tariffs applied by $j$ are changed.

The Gravity Equation

The gravity equation is a description of the equilibrium value of trade at buyers prices. This is $X_{{ij}}^{e} = x_{{ij}}^{e}p_{i}t_{{ij}}$. It is the value associated with the equilibrium in the demand and supply diagram. The equilibrium assumes spatial arbitrage is perfect, so it embeds interdependence of markets and assumes that markets clear — world supply from $i$ equals world demand for goods from $i$.

Aggregate spending on goods by $j$ from all origins ($E_{j}$) affects the position of the demand schedule. Demand $x_{{ij}}^{D}$ rises with aggregate spending $E_{j}$. Since direct proportionality comes close to the trade data, assume for simplicity that demand rises in proportion to $E_{j}$. The larger is $y_{i}$, the further down $j$'s demand curve is the equilibrium intersection with residual supply. Proportionality again is simple and seems likely to come close to the data. Frictions in trade rise with distance and reduce trade. These observations suggested the early gravity equation² as the reduced form solution to the intersection of supply and demand in the demand and supply diagram:

$$X_{{ij}}^{e} = \frac{Y_{i}E_{j}}{G}\frac{1}{d_{{ij}}} \tag{Simple gravity}$$

Here $Y_{i} = p_{i}y_{i}$, the value of $i$'s sales. $G$ is a constant term. The simple gravity equation fits the data well. Specifically consider trade among $N$ countries with $N^{2}$ observed trade flows (including domestic trade). Plotting observed trade against observed values for the variables on the right hand side of the simple gravity equation along with an estimated 'best fit' constant term $G$ displays data points clustered around the 45 degree line.

Extending the simple gravity equation to allow for border frictions improves the fit. Thus replace $1/d_{{ij}}$ with a set of trade friction proxies, including distance, tariffs, trade agreements or not between $i$ and $j$ , contiguity, common language and so forth. The empirical regression analysis estimates the strength of the relationship and its importance to the volume of trade. All such forces are represented by the unobservable theoretical trade friction $t_{{ij}}$ that affects trade flows with trade elasticity $\theta$.

The full gravity model is obtained by imposing economic structure on the simple gravity equation. Elementary economic logic requires that the model add up. This means that (i) the sum of sales by $i$ to all destinations $j$ add up to total sales $Y_{i}$ and (ii) the sum of expenditures by $j$ on goods from all $i$ add up to total expenditure. Moreover, (iii) total world sales must equal total world expenditure. Further suitable restrictions on demand and supply structure yield the structural gravity equation.

The structural gravity equation describes all pairs of trade flows between origins $i$ and destinations $j$ as

$$X_{{ij}}^{e} = \frac{Y_{i}E_{j}}{Y}\left( \frac{t_{{ij}}}{S_{i}P_{j}} \right)^{-\theta} \tag{Gravity}$$

$X_{{ij}}^{e}$ is the equilibrium value of trade purchased by buyers in destination $j$ from sellers in origin $i$. $Y_{i}$ is total sales from $i$ to the world and $E_{j}$ is total purchase by $j$ from the world. $Y$ is world sales, aggregated across country total sales $Y_{i}$. The right hand side of the equation describes the theoretical economic forces that determine the equilibrium value of trade. Compared to the simple gravity equation, the most important change is the presence of $S_{i}P_{j}$.

The first ratio on the right comprises the size effects of origin and destination countries relative to world sales. The size effects term is interpreted as giving the 'as if frictionless' value of trade. To see this interpretation, divide both sides of the gravity equation by $E_{j}$ and suppress the second term. This implies

$$\frac{X_{{ij}}^{e}}{E_{j}} = \frac{Y_{i}}{Y}.$$

This equation holds for all destinations $j$, so it implies that all destinations spend on goods from $i$ an equal share of their total expenditure. This is a reasonable benchmark that would be true of a frictionless world where the prices of goods are equal everywhere, and in addition the tastes (or technologies in the case of intermediate goods) are the same everywhere.

The second ratio on the right hand side of the gravity equation comprises the effect of trade frictions on bilateral trade. $t_{{ij}} > 1$ is a direct bilateral trade friction factor. $S_{i}$ is an index of frictions $t_{{ij}}$ between $i$ and all its destinations. $P_{j}$ is an index of frictions between $j$ and all the origins $i$ it buys from. $\theta > 0$ is the trade elasticity, a parameter quantifying the negative effect on bilateral sales of a rise in the bilateral relative friction $t_{{ij}}/S_{i}P_{j}$.³ $S_{i}$ and $P_{j}$ in the spatial arbitrage equilibrium are consistent with the adding up requirements. This is shown in the next section, and $S_{i}$ and $P_{j}$ are interpreted as sellers' and buyers' incidence respectively.

None of the components of the second, frictions ratio are directly observable. Nevertheless, the observable bilateral trade flows and size variables indicate that frictions are enormously important. Specifically, for cross-border trade, $X_{{ij}}/(Y_{i}E_{j}/Y)$ is far below 1 almost everywhere. Econometric methods are used to dig further, to infer the components of the second ratio from observable variables.

Theoretical relationship in the gravity equation recast as an econometric relationship is typically estimated with a regression of bilateral trade data for a given year on a set of fixed effects for the origin countries (that control for the unobservable $Y_{i}S_{i}^{\theta}$), a set of fixed effects for the destination countries (that control for the unobservable $E_{j}P_{j}^{\theta}$), and a set of proxies for the bilateral trade frictions $t_{{ij}}^{- \theta}$ that affect trade from $i$ to $j$. The proxies for frictions include bilateral distance between $i$ and $j$ and border effects such as tariffs or trade agreements, contiguity, common language, common legal origin, former colonial relationship, and so on. A value of $S_{i}^{\theta}$ is inferred from division of the estimated origin fixed effects by observable $Y_{i}$, and a value $P_{j}^{\theta}$ is inferred from division of the estimated destination fixed effect by observable $E_{j}$. An inferred value of trade elasticity $\theta$ allows direct inference of trade friction $t_{{ij}}$ that can be interpreted as a tariff factor equivalent. A value of $\theta$ also allows direct inference of the values of the friction indexes $S_{i}$ and $P_{j}$ facing sellers and buyers respectively.

Estimated gravity regressions fit the trade data very well. (Indeed the fit is one of the most remarkable successes in all of economics). Distance powerfully reduces trade -- estimated distance elasticities (interpreted as the product of $\theta$ and the elasticity of $t_{{ij}}$ with respect to bilateral distance) cluster around $- 1$. Border effects in general reduce trade substantially, more than can reasonably be accounted for by formal trade policies such as tariffs. Particular interest attaches to inferring the effect of "non-tariff measures" such as regulatory barriers to cross-border trade that potentially can be influenced by trade negotiations.

Gravity and Arbitrage Equilibrium

The explicit treatment above of export supply as a residual supply brings in the adding up constraints of general equilibrium. The gravity model embeds these constraints along with suitable restrictions on demand and supply structure. Return to the gravity equation to understand the role played by incidence.

Gravity equation explains expenditure $p_{{ij}}x_{{ij}} = X_{{ij}}$, an inessential difference from $x_{{ij}}^{D}$ and $x_{ij}^{{RS}}$ in the demand and supply diagram for present purposes. Consider $S_{i}$s and $P_{j}$s that are arbitrary, such as $S_{i} = 1$ and $P_{j} = 1$ for all $i$ and $j$. (Early uses of gravity in fact ignored the incidence terms, effectively setting them equal to 1.) A simple requirement of economic logic is that the model of distribution of goods being represented satisfies two adding up properties:

1. the sum of bilateral sales adds up to total sales, $\sum_{j}^{}X_{{ij}}^{e} = Y_{i}$ for each country $i$; and

2. the sum of bilateral purchases adds up to the total expenditure, $\sum_{i}^{}X_{{ij}}^{e} = E_{j}$ for each country $j$.

Gravity equation does not satisfy the adding up requirements for arbitrary trade frictions $t_{{ij}}$ and arbitrary $S_{i},P_{j}$ -- it would be fortuitous if the adding up restrictions were met. The diagrammatic analysis in the demand and supply diagram (and subsequent discussion of comparative statics of changes in trade frictions) suggest that residual supply and bilateral demand functions shift to adjust toward a solution (equilibrium) where the allocations add up properly.⁴ The adding up requirements (with N countries there are 2N of them) give the requirements of this solution in an equation system form. Under suitable restrictions on demand and supply structure this leads to the gravity equation and sellers' and buyers' incidence equations below. This form also reveals the interpretation of the solution = equilibrium values $S_{i}$ and $P_{j}$ as sellers' and buyers' overall incidence of trade costs. Hoping that the fog of algebra to follow is sufficiently penetrated, this section concludes with drawing out the interpretation.

To see the implications of adding up for sales for $i$, first divide $\sum_{j}^{}X_{ij}^{e} = Y_{i}$ through by $Y_{i}$. Then substitute the right hand side of the gravity equation for $X_{{ij}}^{e}$ in the resulting expression. The result is

$$1 = \sum_{j}^{}\frac{E_{j}}{Y}(t_{{ij}}/S_{i}P_{j})^{- \theta},\ \forall i$$

The implications of adding up for budgets follow exactly analogous steps to yield:

$$1 = \sum_{i}^{}\frac{Y_{i}}{Y}(t_{{ij}}/S_{i}P_{j})^{- \theta},\ \forall j$$

The equations describe the incidence interpretation previously assigned to $S_{i}$ and $P_{j}$. Multiply both sides of the first equation above by $S_{i}^{- \theta}$ and similarly multiply both sides of the second equation above by $P_{j}^{- \theta}$. The results are

$$S_{i}^{- \theta} = \sum_{j}^{}\frac{E_{j}}{Y}\left(\frac{t_{{ij}}}{P_{j}} \right)^{- \theta} \tag{Sellers' incidence}$$

and

$$P_{j}^{- \theta} = \sum_{i}^{}\frac{Y_{i}}{Y}\left( \frac{t_{{ij}}}{S_{i}} \right)^{- \theta}. \tag{Buyers' Incidence}$$

The right hand side of the sellers' incidence equation is a weighted average of the $-\theta$ power transforms of bilateral sellers incidences $(t_{{ij}}/P_{j})^{- \theta}$. Thus $S_{i}$ is interpreted as sellers' incidence facing $i$ overall for the world market. Similarly, the buyer's incidence equation implies that the $- \theta$ power transform of buyers' overall incidence is a weighted average of the $- \theta$ power transforms of bilateral buyers' incidences.

The particular form of gravity equation on its right hand side comes from specifications of demand and supply structure. Several such specifications have been detailed in the academic literature (see Anderson (2011), Arkolakis, Costinot, and Rodríguez-Clare (2012) or Head and Mayer (2014)) but the details are not needed for present purposes.⁵

Multilateral and Bilateral Incidence

In the spatial equilibrium setting, unlike the Economics 101 analysis of incidence in a single isolated market, markets are interconnected, giving rise to both bilateral and multilateral incidence. If as in the demand and supply diagram the ${ij}$ market were to be exactly average, the incidence calculation based on the ${ij}$ market would exactly mimic the partial equilibrium incidence analysis and there would be just sellers' and buyers' incidence.

While convenient for exposition, the average market is not representative -- cross border trade is far below its 'as if frictionless' value while domestic trade is far above it. Thus the gravity equation applied to observed trade flows implies that $t_{{ij}}/S_{i}P_{j} < 1$ for cross-border trade and $t_{{ii}}/S_{i}P_{i} > 1$ for domestic trade.

Despite this difference from incidence in isolated partial equilibrium ($t_{{ij}}/S_{i}P_{j} \neq 1$) the values of $S_{i}$ in spatial equilibrium give a meaningful average value of incidence faced by a seller who simultaneously serves many destinations with differing frictions, size and local competition with sales from other origins. Similarly, the equilibrium values of $P_{j}$ give a meaningful average value of buyers' incidence in purchasing from many origins. Thus $t_{{ij}}/P_{j}$ is interpreted as the bilateral sellers' incidence from $i$ to $j$ and $t_{{ij}}/S_{i}P_{j}$ is interpreted as the ratio of seller $i$'s bilateral incidence to seller $i$'s overall average incidence of trade costs.⁶

Pushing further into differences from the partial equilibrium incidence analysis, only by chance would any single ${ij}$ market calculation of $S_{i}P_{j}$ yield the conclusion that reduction of $t_{{ij}}$ by the proportion $S_{i}P_{j}$ would lower the new incidences to 1 and would raise arbitrage equilibrium $x_{{ij}}^{e}$ to the frictionless equilibrium level $x_{{ij}}^{F}$ as in the demand and supply diagram. What remains a valid homology is that if all $t_{{ij}}$s were to be reduced by $S_{i}P_{j}$, the new incidences would go to 1, the aggregate sales in the new equilibrium would equal the original total sales and aggregate expenditures in the new equilibrium would equal the original total expenditures. In this sense the average bilateral market would replicate the partial equilibrium incidence analysis.

General Equilibrium Simulations

Changes in trade costs shift the equilibrium. The new equilibrium is calculated with a counter-factual simulation. The details of how this is done can now be explained. The gravity module calculates the new arbitrage equilibrium by finding the seller and buyer incidences that are consistent with the new trade costs given the aggregate sales and aggregate expenditures of all countries. Counter-factual simulations of equilibrium changes given the aggregate sales and expenditures are called Modular Trade Impact evaluations by Head and Mayer (2014). Modular impact evaluations are useful when evaluating changes within a sector (for example, trade agreements involving autos only) without requiring treatment of the complicated interactions of sectors.

A general equilibrium superstructure nests the gravity module or modules, interacting to determine new values of the aggregate sales and expenditures given the seller and buyer incidences. In simple models of aggregate trade flows, the general equilibrium superstructure does not much alter the modular trade impact; e.g. Anderson and van Wincoop (2003) report this for their simulation of the effect of removing the Canada-US border.

Arbitrage Equilibrium

Arbitrage equilibrium is subject to the adding up requirements of equilibrium: expenditures on goods from $i$ in all destinations add up to total sales $Y_{i}$ and purchases on goods from all origins add up to expenditures $E_{j}$ in destination $j$. In the gravity model these adding up requirements are satisfied by shifting around the multilateral resistance (incidence) terms $S_{i}$ and $P_{j}$ in the gravity equation. The general equilibrium mechanism of spatial arbitrage finds values of the $2N$ $S_{i}$s and $P_{j}$s that are mutually consistent with each other in the sense that the same $S_{i}$s and $P_{l}$s are used in all diagrams and the demand and residual supply schedules all intersect.

Mechanically this involves finding the simultaneous solution for the 2N $S_{i}$s and $P_{j}$s in the system of 2N equations represented by the incidence equations, reproduced below for convenience. The incidences are colored red to indicate that they are being solved.

$${\color{red}S_i}^{-\theta}=\sum_j \frac{E_j}{Y}\left(\frac{t_{ij}}{\color{red}P_j}\right)^{-\theta} \tag{Sellers' incidence}$$

and

$${\color{red}P_j}^{-\theta}=\sum_i \frac{Y_i}{Y}\left(\frac{t_{ij}}{{\color{red}S_i}}\right)^{-\theta} \tag{Buyers' incidence}$$

Intuitively, finding the equilibrium values requires making a guess on values, checking for disequilibrium in each equation, and then adjusting the values toward new guesses that may come closer to mutual consistency. This is equivalent to shifting around the demand and residual supplies and checking the adding up constraints and adjusting the multilateral resistances to come closer to the constraints. The computer mechanism follows an iterative process to solve for the counter-factual equilibrium values of the incidences. In real spatial system of markets, the economic mechanism is arbitrage that increases supply to under-served markets by reducing supply to over-served markets.

General Equilibrium Superstructure

Full general equilibrium nests the spatial arbitrage equilibrium mechanism of gravity within a superstructure that determines the sales levels ($Y_{i}$s) and the expenditure levels ($E_{j}$s). There are many possible superstructures, partly depending on the focus of the analysis. The simplest focus, developed here, is on aggregate trade. Each country produces a bundle of goods aggregated into a single object, and it purchases other countries' bundles of goods. In this case it is plausible and standard to treat the aggregate bundle as fixed at $y_{i}$ for country $i$, with sales value $p_{i}y_{i} = Y_{i}$.

$p_{i}$ is endogenous, to be determined by the interaction of the superstructure with spatial arbitrage gravity module. It is a convenient standard practice in computational general equilibrium modeling to set the base equilibrium prices $p_{i}^{0} = 1$, hence $y_{i} = Y_{i}^{0}$ where $Y_{i}^{0}$ is observable. Moreover, in general equilibrium modeling, price levels are irrelevant; only relative prices matter. The standard normalization of the set of prices in this context is

$$\sum_{i}^{}p_{i}y_{i}/\sum_{i}^{}y_{i} = 1 \tag{Normalization}$$

The normalization above then implies that the set of prices $\{ p_{i}\}$ in the new equilibrium are relative prices, and $Y = \sum_{i}^{}y_{i}$, the 'real' size of the world economy, is invariant to price changes.

The expenditures (the $E_{j}$s) are necessarily linked to the incomes (the $Y_{j}$s) by the global adding up constraint $\sum_{j}^{}E_{j} = Y$. More dubious mechanisms complete the linkage of individual $E_{j}$s to the $Y_{j}$s.⁷ Balanced trade is the simplest mechanism, $E_{j} = Y_{j}$. The awkward empirical reality of trade imbalance everywhere can be met with a crude static mechanism $E_{j} = \phi_{j}Y_{j}$ subject to $\sum_{j}^{}\phi_{j}Y_{j} = Y$ (Anderson and Yotov, 2016). The initial equilibrium reveals $\phi_{j} = E_{j}^{0}/Y_{j}^{0}$ for each destination $j$ as a set of positive parameters, to be held constant in the simulation. Global adding up is automatically met in the initial equilibrium. Global adding up $\sum_{j}^{}E_{j}^{1} = Y$ in the counter-factual equilibrium implies that

$$E_{j}^{1} = \frac{\phi_{j}Y_{j}^{1}}{\sum_{j}^{}\phi_{j}Y_{j}^{1}}Y$$

An alternative crude procedure to deal with the linkage between incomes and expenditures is to first replace the initial equilibrium with a balanced trade counter-factual equilibrium with the same endowments and preferences and trade costs. From this balanced trade counter-factual equilibrium, the second step injects the counter-factual trade cost (or other) changes calculate a new counter-factual balanced trade equilibrium (Dekle, Eaton, and Kortum 2008). See the Appendix for more technical discussion. This procedure has the advantage of removing effects of trade cost changes that act via changes in the purchasing power of the international transfers. The disadvantage is in removing the connection to the initial observed equilibrium. A further disadvantage appears in the common case when the gravity counter-factual exercise is done for a subset of the sectors in the world economy. Trade imbalance for sectoral studies is large in many cases (because services trade data is limited). The first method is indicated for these cases.

In each country, $p_{i}y_{i} = Y_{i}$ is the total value of resources used in production and distribution. $p_{i}$ is the factory gate price, $y_{i}$ is the total 'produced', with payments for the amount 'melted' in distribution paid to the seller. (A common alternative interpretation is that goods are produced by a stock of labor, hence $p_{i}y_{i} = w_{i}L_{i}$, where $w_{i}$ is the wage in country $i$ and $L_{i}$ is the labor used in production and distribution.)

Aggregate demand by the world for goods from $i$ is a useful concept consistent with structural gravity model (comprising of the gravity equation and the two incidence equations). To model aggregate demand with identical tastes across countries, consider a 'world market' on which a fictitious aggregate buyer faces a 'world price' of $i$ is $p_{i}S_{i}$. The share of the world spending on $i$ is given by $(\beta_{i}p_{i}S_{i})^{- \theta}$. The world market buyers' incidence is equal to 1, all incidence is borne by sellers. Here $\beta_{i} > 0$ is a taste parameter allowing for different shares to be purchased across goods $i$. $\beta_{i}$ is calibrated in the base equilibrium by

$$\beta_{i} = S_{i}^{0}\left( \frac{Y_{i}^{0}}{Y} \right)^{\theta}$$

$\theta$ is a substitution parameter reflecting how sensitive spending is to changes in price, higher values of $\theta$ imply larger percentage falls in spending as the price of $i$ rises.⁸

The world market clearance condition in value terms (aggregate demand = aggregate supply) is

$$p_{i}y_{i} = Y(\beta_{i}p_{i}S_{i})^{- \theta},\ \forall i \tag{World market clearance}$$

Here world income $Y$ is equal to world expenditure. Given values for the sellers' incidences $S_{i}$, world market clearance equations are solved for $p_{i}$:

$$p_{i}^{e} = \left\lbrack \frac{y_{i}}{Y}(\beta_{i}S_{i})^{\theta} \right\rbrack^{- 1/(1 + \theta)}$$

The full set of equilibrium equations includes the incidence equations and world market clearance conditions, subject to the normalization equations. The gravity module includes the incidence equations with given $Y_{i}^{0}$s and $E_{j}^{0}$s.

The counter-factual equilibrium prices are denoted with a tilde and evaluated relative to the base price $= 1$. All other hypothetical changes are measured relative to the base. For example, the model is used to calculate the proportional changes in trade, in welfare, in buyers' and sellers' incidence, etc.

The model implies relative seller price relationship to the proportional change in sellers incidence is:

$${\tilde{p}}_{i} = \left(\frac{{\widetilde{S}}_{i}}{S_{i}^{0}} \right)^{- \theta/(1 + \theta)} \tag{Relative change in price}$$

Then the relative change in sales of $i$ is

$$\frac{{\widetilde{Y}}_{i}}{Y_{i}^{0}} = \left(\frac{{\widetilde{S}}_{i}}{S_{i}^{0}} \right)^{- \theta/(1 + \theta)} \tag{Relative change in sales}$$

The full model is solved using the relative change in sales equation to project the counter-factual value of ${\widetilde{Y}}_{i}$s (and associated ${\widetilde{E}}_{i}$s) into the gravity module (incidence equations). In practice, in this 'one good' per country setup the feedback between relative change in sales equation and the gravity module usually does not result in much change in the seller and buyer incidences. The main action appears to be in the gravity module.

If nothing is changed from the base equilibrium, the model is solved for the base values of $S_{i}$ and $P_{j}$ (and all $p_{i} = 1$). If some $t_{{ij}}$s change, the model solves for the new values of sellers' and buyers' incidences ${\widetilde{S}}_{i}$ and ${\widetilde{P}}_{j}$ and the new factory gate prices ${\tilde{p}}_{i}$.

Then the hypothetical values of bilateral trade can be generated. The trade shifts are interesting objects of policy analysis because they feed into employment projections and profit projections for politically important sectors of the economies of the politically relevant countries. Another interesting object is real income, or welfare.

Welfare Comparative Statics

Welfare measures all are based on the idea of real income. In the gravity setup here, real income is sensibly defined as $p_{i}y_{i}/\Pi_{i}$, nominal income divided by a price index of consumption $\Pi_{i}$. For comparative statics the meaningful comparison is the ratio of counter-factual real income to base real income. Since the endowment $y_{i}$ does not change, the welfare proportional change is simply

$$\frac{{\widetilde{W}}_{i}}{W_{i}^{0}} = \frac{{\tilde{p}}_{i}/{\widetilde{\Pi}}_{i}}{p_{i}^{0}/\Pi_{i}^{0}}$$

The buyers' price index $\Pi_{i}$ in the case of identical tastes (see footnote) is equal to the buyers' incidence $P_{i}$ (Anderson, 2011). In any case, the buyers' incidence is an important component of the buyers' price index. Use the relative change in price equation for the relative change in sellers' price. The welfare change is thus:

$$\frac{{\widetilde{W}}_{i}}{W_{i}^{0}} = \left( \frac{{\widetilde{S}}_{i}}{S_{i}^{0}} \right)^{- \theta/(1 + \theta)}\frac{P_{i}^{0}}{{\widetilde{P}}_{i}} \tag{Welfare change}$$

Appendix

Superstructure Extensions

More elaborate superstructures are sometimes needed for analysis. In all cases, sectoral gravity modules nest inside the resulting full general equilibrium models.

Simulation models with trade imbalance treated in a less crude way than in the text might embed the preceding gravity mechanism into multiple time periods to allow for external borrowing and lending. This requires another layer of superstructure for international lending/borrowing and the associated inter-temporal trade. Standard practice avoids this complexity, partly justified by there being no agreement on how to build such models in a way that can come close to the observed data on international lending.

A significant complication to the link of expenditures to sales incomes arises when tariff revenues are important. Part of $t_{{ij}}$ is due to the ad valorem tariff factor $1 + \tau_{{ij}}$. Then tariff revenue is

$$R_{j} = \sum_{i \neq j}^{}\frac{\tau_{{ij}}}{1 + \tau_{{ij}}}X_{{ij}}^{e}.$$

Expenditure $E_{j}$ with balanced trade is met by income $Y_{j}$ plus tariff revenue $R_{j}$, so expenditure becomes more richly endogenous. (Essentially there is a multiplier effect at work where more income raises imports which raises more revenue.) It useful to abstract from this complication when tariff rates $\tau_{{ij}}$ are small. This is the case for many sectors, especially in rich countries. Nevertheless, some of the very large border resistances to trade observed in gravity research may be associated with rents that are similar to tariff revenue. Unfortunately the rents are ordinarily not observable.

More complications arise when multi-sector models are the focus. The analog to the fixed endowments $y_{i}$ is a multi-sector fixed endowments assumption that fixes the sectoral activities $y_{i}^{k}$ for all sectors $k$. An alternative is to model sectoral resource reallocation with $y_{i}^{k}$s that vary with the sellers' prices $p_{i}^{k}$. On the demand side, aggregate country expenditures are allocated to sectoral aggregate expenditures with mechanisms that require structure. Intermediate goods and input-output linkages require treatment in these settings, having both a supply side and a demand (for inputs) side.

---

1. The transition path from the initial disequilibrium to the arbitrage equilibrium is the subject of a literature on spatial price arbitrage that uses gravity structure with data on prices at points in time that are close together. The gravity model of trade, in contrast, assumes arbitrage equilibrium and uses gravity structure for trade flows over an interval of time (usually a year) taken to reflect long run equilibrium. Trade policy analysis is appropriately focused on long run considerations because trade policy is usually set with long term commitments. Empirical gravity models interpret the inevitable arbitrage imperfections in observed annual trade flows as unsystematic, hence unrelated to the model's determinants of trade. ↩

2. "Gravity" because the right hand side is proportional to the product of the economic masses and falls with distance. In the data, trade is close to inversely proportional to distance as in the simple gravity equation. Newton's Law in physics requires the square of distance in the denominator of the simple gravity equation with $1/G$ being the gravitational constant. ↩

3. There are several economic structures that lead to the gravity equation, with different interpretations of $\theta$. For more discussion see Anderson (2011) or Head and Mayer (2014). ↩

4. The implication is the gravity equation is plausible as a description of spatial arbitrage equilibrium. The impact of the set of bilateral trade frictions gets aggregated into an overall average, and the impact of the bilateral friction on equilibrium trade involves bilateral relative to multilateral (overall) friction. For that reason, $S_{i}$ and $P_{j}$ are called multilateral resistances. ↩

5. The early gravity equations used in economics did not allow for $S_{i}$ and $P_{j}$, hence did not satisfy elementary economic consistency requirements. Anderson (1979) derived a theory-consistent gravity equation, but an econometrically operational version was not available until Anderson and van Wincoop (2003). The early form of the equation was borrowed from Newtonian physics analysis of gravitational force in the 2 body problem. The N body problem in physics has no neat reduced form like the gravity equation, so it was not useful for clues about modeling a many country trade problem. Finishing the connection, note that $S_{i}$ and $P_{j}$ are necessary even in a 2 country world because each country sells in two markets, domestic and foreign. Thus it presents a four body problem in the physics analogy. ↩

6. The alternative interpretation of $t_{{ij}}/S_{i}P_{j}$ is that $t_{{ij}}/S_{i}$ is buyer $j$'s bilateral incidence of trade costs; and $t_{{ij}}/S_{i}P_{j}$ is the ratio of buyer $j$'s bilateral incidence on purchase from $i$ to buyer $j$'s overall average incidence of trade costs. ↩

7. The difficulty in settling on a linkage structure comes from unsettled dynamics and random shocks. International borrowing/lending necessarily associated with trade imbalances in principle reflects both intertemporal trade and accommodation to random shocks. There is no settled mechanism for modeling international borrowing/lending. The contrast to static gravity modeling is sharp. ↩

8. This setup is based on a Constant Elasticity of Substitution (CES) demand structure. If tastes are indeed identical, the share of spending on good $i$ in each country $j$ is given by $(\beta_{i}p_{i}t_{{ij}}/P_{j})^{- \theta}$. $P_{j}$ in this context is interpreted as the CES price index solved from summing the shares (equal to 1) and multiplying both sides by $P_{j}^{- \theta}$: $P_{j}^{- \theta} = \sum_{i}^{}(\beta_{i}p_{i}t_{{ij}})^{- \theta}$. See Anderson (2011) for more details. The buyers' incidence interpretation of $P_{j}$ in the text is thus supplemented with the CES price index interpretation. If tastes are not identical across countries, $\beta_{{ij}} \neq \beta_{i}$ for the aggregate representative buyer. In this case the CES price index for country $j$ deviates from its buyers' incidence. Moreover, the effect of taste differences on trade flows is combined with trade frictions. Gravity methods alone cannot disentangle the two forces. Decomposition of trade frictions into taste bias and trade cost components is irrelevant to trade policy comparative statics, though it is important for some purposes. ↩