May 2018
The authors are staff with the Office of Industries of the U.S. International Trade Commission (USITC). Office of Industries working papers are the result of the ongoing professional research of USITC staff and solely represent the opinions and professional research of individual authors. These papers do not necessarily represent the views of the U.S. International Trade Commission or any of its individual Commissioners. Working papers are circulated to promote the active exchange of ideas between USITC staff and recognized experts outside the USITC, and to promote professional development of office staff by encouraging outside professional critique of staff research. Please direct all correspondence to: Isaac Wohl, Office of Industries, U.S. International Trade Commission, 500 E Street, SW, Washington, DC 20436, telephone: (202) 205-3356, fax: (202) 205-2359, email: isaac.wohl@usitc.gov.
This paper presents a very preliminary attempt to analyze international trade data with neural networks.1 We use a dataset assembled for an international trade gravity model, which has bilateral trade as the dependent variable, and the distance between countries; the exporter’s GDP; the importer’s GDP; dummy variables indicating whether the countries share a language, border, colonial relationship, or trade agreement; and country or country-year fixed effects as independent variables. The paper provides a brief overview of gravity models, explains neural networks, discusses the difference between hypothesis testing and prediction, and presents the results of our analysis. We divide the data randomly into a training set and a test set; use the training set data to create an OLS estimator, a Poisson pseudo-maximum likelihood estimator, and a neural network; and then use the test data to measure how well the different methods generalize to new data. We compare a baseline model, a model with country fixed effects, and a model with country-year fixed effects. The estimator that yields the most accurate out-of-sample estimates is the neural network with country fixed effects, as seen in a comparison of root mean squared errors. We then compare neural network predictions with actual trade between the United States and its major trading partners outside of the sample period. Finally we suggest directions in future research.
Large sets of economic data are increasingly available, and machine learning tools, including neural networks, offer effective and interesting ways to model complex relationships in these datasets.2 Neural networks are “black box” models in that their parameters cannot always be easily interpreted, for example the way coefficients in some regressions can be interpreted as elasticities. However, they are good at combining variables in complex non-linear ways that can generate fairly accurate predictions.
This paper applies neural networks to international trade data. It does not break new ground in designing neural networks or constructing gravity model datasets; it simply applies one to the other. The goal is to examine whether trade between countries can be accurately predicted with a limited amount of data.
This paper is organized as follows: it gives an overview of gravity models, discusses neural networks, compares hypothesis testing with prediction, explains the methods used in this analysis, presents the results, compares neural network predictions with actual trade between the United States and its major trading partners, and proposes directions for future research.
Gravity models are a workhorse tool of international trade analysis. Their basic insight is that trade between two countries is expected to be correlated with their respective sizes (measured by their GDPs) and the distance between them. This model is intuitive, flexible, has strong theoretical foundations, and can make reasonably accurate predictions of international trade.3
A simple gravity model can be augmented in various ways. Gravity models often include dummy variables that indicate whether the trade partners share a border, a language, a colonial relationship, or a regional trade agreement. Anderson and van Wincoop noted that gravity models should account for multilateral resistance, because relative trade costs—not just absolute costs—matter.4 Gravity models can capture multilateral resistance, as well as other country-specific historical, cultural, and geographic factors, by using country fixed effects: dummy variables for each country exporter and each country importer.5 Some gravity models use country-year fixed effects, country-pair fixed effects, or both.
Gravity models can take the form of Ordinary Least Squares (OLS) estimators, such as:
…or, with the addition of exporter and importer fixed effects:
…or, with exporter-year and importer-year fixed effects:
This last equation uses a large number of variables but avoids the assumption that country-specific factors are constant over time. The exporter GDP and importer GDP variables are absorbed by the country-year dummies and are therefore dropped.
One challenge is that when trade flows are transformed into logarithmic form, observations with zero trade flows are dropped.6 One way to handle this (following Eichengreen and Irwin) is to transform trade between country and country into , so that zero trade flows become slightly positive, and use that as the dependent variable in an OLS estimator.7 This approach makes it a little more difficult to interpret the coefficients, but avoids the loss of observations.8
Another approach, proposed by Santos Silva and Tenreyro, is to use Poisson pseudo maximum likelihood (PPML), a non-linear estimator that does not rely on a log transformation of trade flows.9 The PPML estimator is recommended by Piermartini and Yotov among others as a best practice for estimating gravity equations, because it provides unbiased and consistent estimates even with significant heteroscedasticity in the data and a large proportion of zero trade values.10
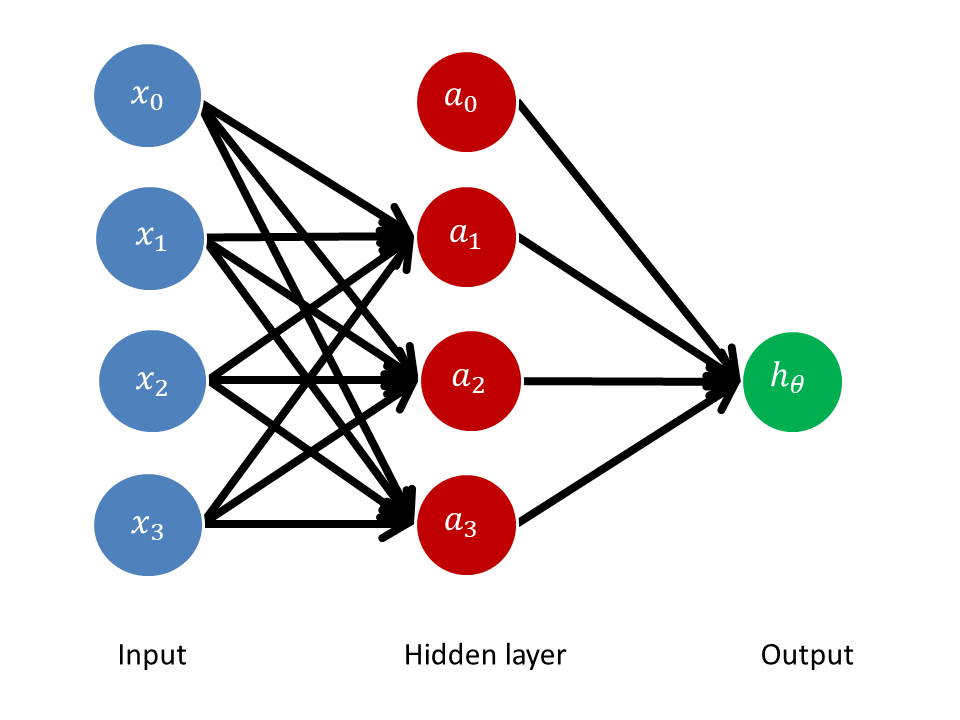
Neural networks are statistical models that can find and test relationships in large datasets.11 They are analogous to a set of brain neurons: each neuron receives inputs from some neurons and provides outputs to other neurons. Neural networks involve an input layer of data (i.e., a set of independent variables), “hidden layers” of nodes, and an output layer that computes final values. The strength of each connection is quantified with a weight, or coefficient. Each node is a function of weighted inputs, and then is itself weighted and used in a function that calculates the output. “Forward propagation” is the process of computing a final value from initial data using these weights. The hidden layers let neural networks combine inputs in complex nonlinear ways, allowing computations that would not be possible with a single layer.12 A neural network with just one hidden layer can approximate any continuous function, no matter how complicated.13
Neural networks “learn” by comparing the outputs they generate to the true values of the dependent variable, and then adjusting their weights to minimize the errors. They are not given a stipulated relationship between variables or a set of rules for producing the output; they are just provided with the inputs, the desired output, and a network architecture. In backpropagation networks, the network starts with random weights, produces an output, compares that output with the desired output, and passes an error signal back through the network. The weights are changed, a new output is produced with the new weights, and the new error is assessed. This cycle is repeated, adjusting the weights each time, so the model makes better and better predictions and the average error approaches zero. These adjustments are made by an iterative algorithm that converges at an optimum.14
Figure 1 illustrates forward propagation in a neural network with a single hidden layer:
Figure 1: Neural network with one hidden layer

Each node in the hidden layer receives weighted inputs from each node in the input layer, and the output receives weighted inputs from the hidden layer. The number of input nodes reflects the number of independent variables in the dataset. (Most networks also include “bias units,” and , that are always equal to one, and are not connected to previous layers but do contribute to the network’s output. They are analogous to constant terms in linear functions; they give the network the flexibility to shift, and not just reshape, the function.) Figure 1 shows a neural network with one hidden layer comprising three nodes (four including the bias unit), but neural networks can include many hidden layers with many nodes. The output is the final value of the network. Here, each node in the hidden layer is a function of weighted inputs:
…and the output is a function of weighted nodes:
…where is a matrix of weights (or parameters) mapping from layer to layer , and is the “activation function” that operates from one layer to another. Neural networks often use a sigmoid (or logistic) activation function (figure 2):
Figure 2: Sigmoid function
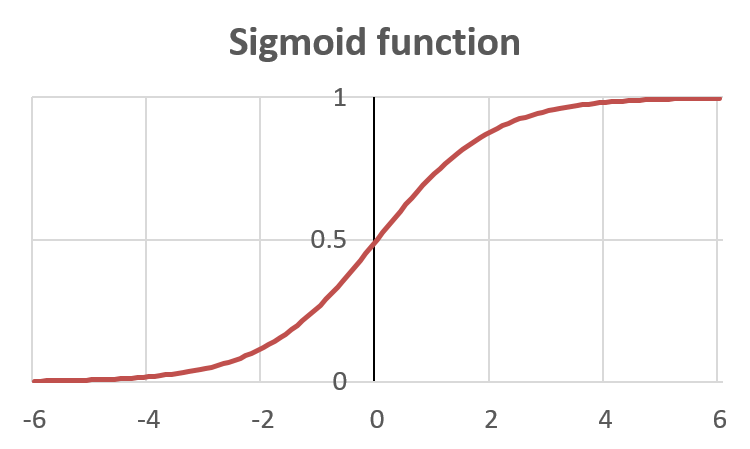
Without a hidden layer, the neural network would simply be a logistic regression, mapping the weighted inputs to the output. Here, though, the output is a logistic regression using the hidden layer nodes as inputs, and each hidden layer node is itself a logistic regression of the previous layer’s inputs, with each regression using a different set of parameters.
The network “learns its own features” in that it generates , , and . That is, it generates the parameters () that map the inputs () to the hidden nodes (). It learns these features with a cost function, which measures the error of the neural network’s output as compared to the given values of . These errors are calculated “right to left” by using the error terms in the last layer to compute the error terms in the next-to-last layer.15 An optimization function, such as the Limited-memory Broyden-Fletcher-Goldfarb-Shanno algorithm (L-BFGS), tries to minimize the cost function. Intuitively, this resembles the way OLS estimators measure, and try to minimize, the residual between the estimated value and the actual value.
In this paper, we use standard gravity model variables (distance, GDP, border, language, colonial relationship, and trade agreement) as inputs. The hidden nodes are functions of these weighted inputs. And the output is a function of the weighted hidden nodes. The neural network adjusts these weights so that the calculated outputs approach the actual values of bilateral trade.
OLS and similar estimators let us test hypotheses about the significance of different variables. For example, a gravity model tests the null hypothesis that a change in distance has no correlation with a change in exports, holding other factors constant. Gravity models usually reject this hypothesis: distance typically has a negative coefficient with an extremely negative t-score, meaning that if the null hypothesis was true, and distance has no correlation with trade, the probability of obtaining a coefficient as large as the one observed purely by random sampling variation is less than 5 percent (and generally less than 1 percent). It is interesting that distance is significantly correlated with trade when holding countries constant over time (country fixed effects), and even when holding countries constant in each year (country-year fixed effects). It is also interesting that distance is significantly correlated with trade in services that incur no shipment costs.16 Here, a theory about international trade specifies a relationship between variables, and data is then collected and analyzed through the lens of that theory.
Prediction asks a different kind of question: what is going to happen, not how will it happen. Prediction techniques estimate the conditional value of a dependent variable given a set of independent variables. They do not necessarily make assumptions about the structure of the relationship or the chain of causality, and neural networks in particular allow for complex nonlinear relationships between dependent and independent variables (for example, by running combinations of inputs through activation functions, and then combining those outputs and running them through another layer of activation functions). A neural network is optimized by altering parameters and assessing the effect of such alterations using the sole criteria of whether it makes the predicted value of the dependent variable more or less accurate. For that reason it is difficult to use neural networks to formally test hypotheses about the significance of variables: the complex combination of the neural networks’ inputs means that the relationships between the variables are not easily interpretable. In this respect neural networks are something of a black box. In cases where the research question is to predict an outcome, however, we can compare the predictive abilities of neural networks against those of different analytical methods. The accuracy of predictions can be measured by the gap between the estimated value and the actual value, for example by calculating the root mean squared error.
There is a risk of developing complex estimators that fit sample data very well but are not very good at making out-of-sample predictions. This generalization problem can be ameliorated by dividing datasets randomly into training sets and test sets. Parameters are established using training datasets, and then the estimators and neural networks are applied to the test datasets. This lets us measure how well the model predicts the test data outputs.
Our international trade dataset combines World Bank data17 with trade and gravity model data that was assembled and kindly provided by Yotov (2016) using data from COMTRADE18 and CEPII.19 It includes aggregate bilateral manufacturing trade data by year and the standard gravity variables of GDP, distance, border, language, colonial ties, and trade agreements. For exporter , importer , and year ,
For example, the observation for Argentina’s exports to Australia in 1986 is rendered as
...and
Here, Argentina and Australia are 12,045km apart (using the Great Circle Distance formula); their GDPs in 1986 were $215b and $524b respectively; they don’t share a border, language, or colonial relationship, and had no trade agreement as of 1986; and the value of Argentina’s exports to Australia that year was $28m. Our dataset comprises 91,094 observations of trade between 68 partners from 1986 to 2006.20
We divide the dataset randomly into training observations (70 percent of the dataset) and test observations (30 percent of the dataset). We use the training dataset to develop the estimators, then feed the independent variables from the test dataset into those estimators to generate predicted trade values for the out-of-sample observations.
For the OLS estimator, we use the natural log of the continuous variables (distance, exporter’s GDP, and importer’s GDP). The dependent variable is the natural log of trade plus $1, to avoid the loss of observations.
For the PPML estimator, we use the natural log of the continuous independent variables, and untransformed trade values as the dependent variable. We use the PPML command developed for Stata by Santos Silva and Tenreyro.
For the neural network, we standardize the continuous variables (trade, distance, exporter’s GDP, and importer’s GDP), scaling them so that their means equal zero and their standard deviations equal one. (Neural networks are generally sensitive to scaling because the sigmoid function approaches a asymptote as values deviate from zero.) We use the multi-layer perceptron regressor in Python’s scikit-learn package, with the sigmoid function as the activation function for the hidden layers and the L-BFGS solver for weight optimization. The regressor trains iteratively, computing the loss functions and updating its parameters. We use one hidden layer with 20 nodes.21
We measure the accuracy of the out-of-sample predictions using the root mean square error (RMSE), which computes the square root of the average of squared errors between the predicted values and the actual values:
…where is the predicted observation, is the actual observation, and is the number of observations.
Table 1 shows the results. For the baseline dataset, the OLS estimator has an out-of-sample root mean squared error of $55.0 billion, the PPML estimator has an out-of-sample RMSE of $2.8 billion, and the neural network has an out-of-sample RMSE of $1.8 billion. For the dataset with country fixed effects, the OLS estimator has an out-of-sample RMSE of $50.8 billion, the PPML estimator has an out-of-sample RMSE of $1.6 billion, and the neural network has an out-of-sample RMSE of $744 million. For the dataset with country-year fixed effects, the OLS estimator has an out-of-sample RMSE of $50.3 billion, and the PPML estimator and neural network both have out-of-sample RMSEs of $2.3 billion. These analyses were repeated several times, allowing for variation in the random training-test division and in the development of the neural network, and these outcomes are representative.
Table 1: Trade predictions using different estimators
| OLS | PPML | Neural network | |
| Adjustments and architecture |
Dependent variable: Natural log of distance and GDP |
Dependent variable: Natural log of distance and GDP |
Trade, distance, and GDP standardized (mean = 0, standard deviation = 1) 1 hidden layer, 20 nodes |
| Baseline model, 7 variables: | |||
| Out-of-sample root mean squared error (million USD) |
$54,997 | $2,846 | $1,797 |
| Country fixed effects, 143 variables: | |||
| Out-of-sample root mean squared error (million USD) |
$50,834 | $1,560 | $744 |
| Country-year fixed effects, 2,791 variables: | |||
| Out-of-sample root mean squared error (million USD) |
$50,327 | $2,302 | $2,328 |
It is noteworthy that for PPML and neural network estimators the out-of-sample error is higher when using country-year fixed effects compared to country fixed effects. This suggests that using country-year fixed effects makes the models more specific to training data, and less generalizable to out-of-sample data. The matrix of country-year fixed effects is very sparse: there are only 182,188 nonzero elements and 253,605,696 zero elements, giving it a density (i.e., ratio of nonzero to zero elements) of 0.07 percent. In contrast, the matrix of country fixed effects is less sparse, with a density of 1.4 percent. When using country-year fixed effects, the estimators are generating parameters for each dummy variable based on a very small sample.
The neural network with country fixed effects has the greatest predictive accuracy among the models. It achieves a 52 percent reduction in out-of-sample RMSE compared to the PPML estimator on the same dataset, and a 99 percent reduction compared to the OLS estimator. It is expected that neural networks would have equal or better predictive accuracy than the other estimators, since neural networks with the right specifications can approximate any continuous function, linear or non-linear (see above). The size of the gap in predictive accuracy suggests that neural networks are capturing non-linear interactions of independent variables that affect trade in ways not captured by OLS or PPML models. One point of note is that the RMSE of the neural network without country fixed effects is close to the RMSE of the PPML estimator with country fixed effects: neural networks using only seven variables can generate predictions almost as accurate as PPML estimators using 143 variables. Neural networks can efficiently use a small number of economic, geographic, and historical variables to generate fairly accurate predictions about international trade.
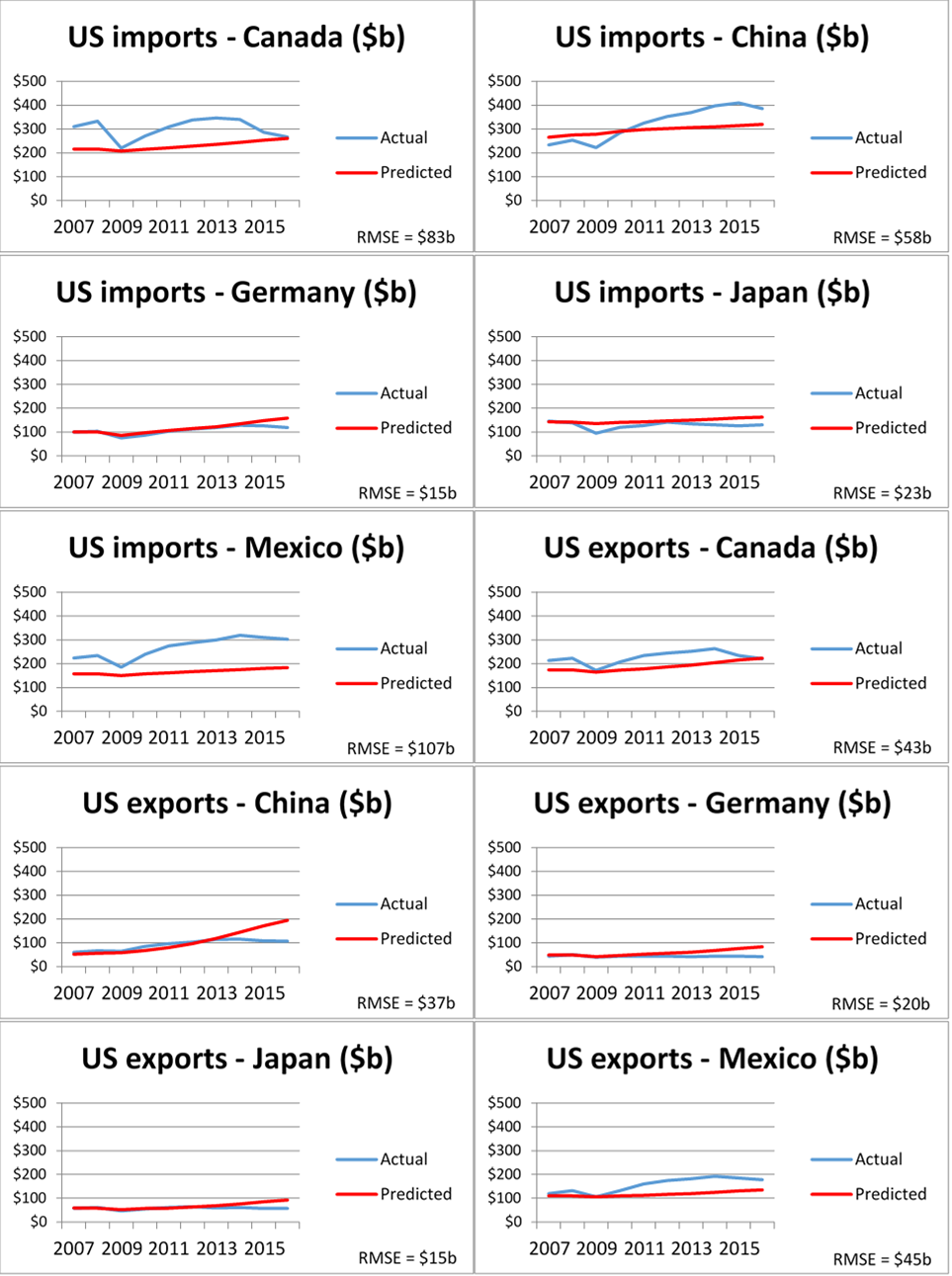
To illustrate one forecasting application, we trained the neural network on the full dataset with country fixed effects from 1986 to 2006 and used it to predict trade between the United States and its major trading partners between 2007 and 2016. We provided the neural network with the actual GDPs of the United States and its trading partners during that period, without otherwise readjusting the model. Figure 3 shows the results. The neural network’s estimations are reasonably close to actual trade values even ten years beyond the training period.
Figure 3: Neural network predictions versus actual trade
It is useful to understand why trade happens the way it happens, a theoretical inquiry that can be facilitated by gravity models with traditional specifications. It is also useful to be able to predict trade between two countries with a high degree of accuracy, a practical inquiry that can be facilitated by neural networks. Policymakers, researchers, and firms can all benefit from accurate forecasts about international trade.22
One direction for future research is to use neural networks to predict the effects of trade agreements or other trade policies. Another is to further explore how changes in inputs and model architecture affect predictive accuracy. A third is to apply this same exercise to trade in specific commodities, manufactures, and services, instead of total trade. A fourth is to examine more closely why trade between some countries in some circumstances (such as U.S. imports from Mexico and Canada in figure 3) deviate more from predictions than others. A final direction is to continuously train neural networks using past trade data, generate predictions of future trade, and track the accuracy of such predictions going forward. This can contribute to further improvement in predictions, and analyses that yield inaccurate predictions may lead to discoveries that the models themselves have shortcomings, or that something in the world has changed.
Anderson, James; Ingo Borchert; Aaditya Mattoo; and Yoto Yotov. “Dark Costs, Missing Data: Shedding Some Light on Services Trade.” World Bank Policy Research Working Paper, October 2015. http://documents.worldbank.org/curated/en/991861467998824181/Dark-costs-missing-data-shedding-some-light-on-services-trade
Anderson, James and Eric van Wincoop. “Gravity with Gravitas: A Solution to the Border Puzzle.” American Economic Review, vol. 93, no. 1, March 2003. https://www.aeaweb.org/articles?id=10.1257/000282803321455214
Bergstrand, Jeffrey and Scott Baier. “Bonus Vetus OLS: A Simple Method for Approximating International Trade-Cost Effects Using the Gravity Equation.” Journal of International Economics, vol. 77, February 2009. https://www.researchgate.net/publication/23775985_Bonus_Vetus_OLS_A_Simple_Method_for_Approximating_International_Trade-Cost_Effects_Using_the_Gravity_Equation
Comp.ai.neural-nets FAQ. “Section – How Many Hidden Units Should I Use?” FAQs.org. http://www.faqs.org/faqs/ai-faq/neural-nets/part3/section-10.html (retrieved December 1, 2017).
Cybenko, George. “Approximations by Superpositions of Sigmoidal Functions.” Mathematics of Control, Signals, and Systems, vol. 2, no. 4, 1989. http://web.eecs.umich.edu/~cscott/smlrg/approx_by_superposition.pdf
Eichengreen, Barry and Douglas Irwin. Trade Blocs, Currency Blocs and the Reorientation of World Trade in the 1930s.” Journal of International Economics, vol. 38, July 1995. http://www.dartmouth.edu/~dirwin/docs/Blocs.pdf
Friedman, Jerome; Robert Ribshirani; and Trevor Hastie. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. Springer, 2001. https://statweb.stanford.edu/~tibs/ElemStatLearn/printings/ESLII_print10.pdf
Head, Keith and Thierry Mayer. “Gravity Equations: Workhorse, Toolkit, and Cookbook.” CEPII Working Paper, September 2013. http://www.cepii.fr/pdf_pub/wp/2013/wp2013-27.pdf
MHI. The 2017 MHI Annual Industry Report- Next-Generation Supply Chains; Digital, On-Demand, and Always-On. MHI & Deloitte, 2017. https://www.mhi.org/publications/report
Ng, Andrew. Machine Learning. Coursera, 2016. https://www.coursera.org/learn/machine-learning
Piermartini, Roberta and Yoto Yotov. “Estimating Trade Policy Effects with Structural Gravity.” WTO Working Paper, 2016. https://www.wto.org/English/res_e/reser_e/ersd201610_e.pdf
Santos Silva, J. M. C. and Silvana Tenreyro. “The Log of Gravity.” Review of Economics and Statistics, vol. 88, no. 4, November 2006. http://www.mitpressjournals.org/doi/abs/10.1162/rest.88.4.641
Varian, Hal. “Big Data: New Tricks for Econometrics.” Journal of Economic Perspectives, vol. 28, no. 2, 2014. https://www.aeaweb.org/articles?id=10.1257/jep.28.2.3
Yotov, Yoto. “A Simple Solution to the Distance Puzzle in International Trade.” Economics Letters, vol. 117, no. 3, December 2012. https://www.sciencedirect.com/science/article/pii/S0165176512004673
Yotov, Yoto. “Gravity Training Course.” USITC, August 2016.
The authors would like to thank David Coffin, John Fry, Peter Herman, Tamar Khachaturian, Martha Lawless, Jen Powell, David Riker, Monica Sanders, and Yoto Yotov.↩
Varian, “Big Data,” 2014.↩
Gravity models have faced various criticisms. For example, most gravity model estimations have found a persistently strong negative effect of distance on international trade since the 1950s, contrary to empirical evidence on falling transport costs and globalization. However, a 2012 paper by Yotov finds that gravity models do show a declining effect of distance on trade over time when they account for internal trade costs. Yotov, “A Simple Solution to the Distance Puzzle in International Trade,” 2012.↩
Anderson and van Wincoop, “Gravity with Gravitas,” March 2003. For example, Australia and New Zealand would be expected to trade more with each other than the absolute distance between them would indicate, because both countries are geographically distant from other trading partners.↩
However, one disadvantage of this method is that country fixed effects will absorb any time-invariant country-specific factor of interest. Baier and Bergstrand, “Bonus Vetus OLS,” February 2009.↩
Piermartini and Yotov, “Estimating Trade Policy Effects with Structural Gravity,” 2016.↩
Eichengreen and Irwin, “Trade Blocs, Currency Blocs and the Reorientation of World Trade in the 1930s,” July 1995.↩
Head and Mayer, “Gravity Equations,” September 2013.↩
Santos Silva and Tenreyro, “The Log of Gravity,” November 2006.↩
Piermartini and Yotov, “Estimating Trade Policy Effects with Structural Gravity,” 2016.↩
The discussion in this section follows Ng, Machine Learning, 2016.↩
A classic example with logical functions is the “exclusive or” problem. A one-layer network using simple logical operators (like “and,” “or,” and “not and”) cannot compute the function “either A or B, but not both.” However, this function can be computed with a hidden layer. The first layer can determine whether (1) “at least one element is true,” and (2) “not all elements are true.” The second layer can determine whether “both (1) and (2) are true.”↩
Cybenko, “Approximations by Superpositions of Sigmoidal Functions,” 1989.↩
A typical application of neural networks is handwriting recognition. Computers can scan handwritten numbers and encode their greyscale pixel values, but because of the wide variety of handwriting styles it is difficult to come up with a comprehensive set of steps and rules for recognizing numbers (e.g., “the number 8 consists of two circles stacked vertically”). A different approach is not to stipulate any rules at all, but instead to use the pixel values as inputs, restrict outputs to digits 0 through 9, and train the neural network. “Training” means letting the neural network assign weights to the inputs and produce one of the ten outputs, then telling the network whether it got the answer right or wrong. In response, the neural network will adjust its weights. By training a neural network algorithm over millions of examples, it can arrive at a set of weights that increase its accuracy to nearly 100%. Commercial neural networks are commonly used for handwriting recognition by banks and post offices. Friedman, Ribshirani, and Hastie, The Elements of Statistical Learning, 2001, 4.↩
In the above example, the output error could be used to calculate the errors in the hidden layers using the matrix and the derivative of the activation function: ↩
Anderson et al., “Dark Costs, Missing Data,” October 2015. This paper finds that the effects of distance on services trade vary widely across sectors and are highly nonlinear.↩
http://www.cepii.fr/CEPII/en/bdd_modele/presentation.asp?id=19↩
Some years are missing for Hungary, Kuwait, Poland, Qatar, Romania, and Tanzania.↩
Generally there is no straightforward way to determine the best number of hidden units. Adding units improves the performance of the neural network on the training data but can increase errors in test data as the network becomes less generalizable. Here we settled on one hidden layer with 20 nodes after experimentation, but our results are robust to other architectures. Comp.ai.neural-nets FAQ, “Section – How Many Hidden Units Should I Use?”↩
In one survey, 17 percent of manufacturing and supply chain companies said they are currently using predictive analysis in their business operations, and 79 percent said they will within the next five years. MHI, 2017 MHI Annual Industry Report, 2017.↩