AN INTRODUCTION TO PARTIAL EQUILIBRIUM

MODELING OF TRADE POLICY

Ross Hallren

David Riker

ECONOMICS WORKING PAPER SERIES

Working Paper 2017-07-B

U.S. INTERNATIONAL TRADE COMMISSION

500 E Street SW

Washington, DC 20436

July 2017

The authors are grateful to Andre Barbe, Justino De La Cruz and Craig Thomsen for helpful comments and suggestions.

Office of Economics working papers are the result of ongoing professional research of USITC Staff and are solely meant to represent the opinions and professional research of individual authors. These papers are not meant to represent in any way the views of the U.S. International Trade Commission or any of its individual Commissioners. Working papers are circulated to promote the active exchange of ideas between USITC Staff and recognized experts outside the USITC and to promote professional development of Office Staff by encouraging outside professional critique of staff research.

An Introduction to Partial Equilibrium Modeling of Trade Policy

Ross Hallren and David Riker

Office of Economics Working Paper 2017-07-B

July 2017

ABSTRACT

This paper introduces the theoretical framework and data inputs of a basic partial equilibrium model of how an industry’s import volumes, domestic shipments, and prices would change in response to a change in trade policy. We start with an overview of economic models used to estimate the effects of tariffs and quotas on imports. Then we go step-by-step through the equations that we use to calculate the changes in the economic outcomes and discuss the data required to run the model. Next, we report several illustrative applications. We conclude with a discussion of several extensions of the basic model.

Ross Hallren

Office of Economic, Research Division

Ross.Hallren@usitc.gov

David Riker

Office of Economics, Research Division

David.Riker@usitc.gov

1. Introduction

An economic model is a system of equations that can be used to quantify the changes in economic outcomes resulting from a change in policy. In this case, the economic outcomes that we analyze are import volumes, domestic shipments, and prices in a specific industry and the policies are tariffs and quotas on industry imports.

In trade policy analysis, models are often used to create forward-looking projections of the economic effects of policy changes that have not yet occurred. Model-based simulations are well-suited for this type of prospective analysis. Simulations isolate the effect of a trade policy by changing the policy (e.g., the tariff rate), assuming that other supply and demand fundamentals do not change. The parameters of the model are calibrated to current or recent data for the industry. The economic impact of the policy is calculated as the difference between the model’s predictions for market prices and quantities after the policy change and the baseline values of market prices and quantities before (or absent) the policy change. In this paper, we focus on two common trade policies: ad valorem tariffs and import quotas. [1]

Simulation models of trade policy vary in complexity. Computable general equilibrium (CGE) models are elaborate models that require a lot of data and are sometimes difficult to run, but they are a very useful analytical tool when the policy changes under consideration affect many different sectors in the economy and policy makers are requesting an estimate of economy-wide effects of the policy changes. On the other hand, when the policy changes are more narrowly focused on a single industry, smaller targeted industry-specific models can be the right tool because they are easy to set up, modify, and operate, and they generally require fewer data inputs. This paper introduces the basic industry-specific model.

We make a number of assumptions to simplify the equations in our industry-specific model. Chief among these simplifications, we assume that aggregate expenditure levels and prices in other industries in the economy do not change with the changes in trade policy. This partial equilibrium approach is an appropriate simplification when the industry is only a small share of the overall economy.

The rest of this paper is organized into four parts. Section 2 describes the equations and assumptions of the model. Section 3 discusses the data inputs. Section 4 presents illustrative applications that analyze tariff reductions. Section 5 presents applications that analyze quota increases. Section 6 concludes with a discussion of extensions of the basic model that incorporate additional information about the structure of the specific industry.

2. Modeling Framework

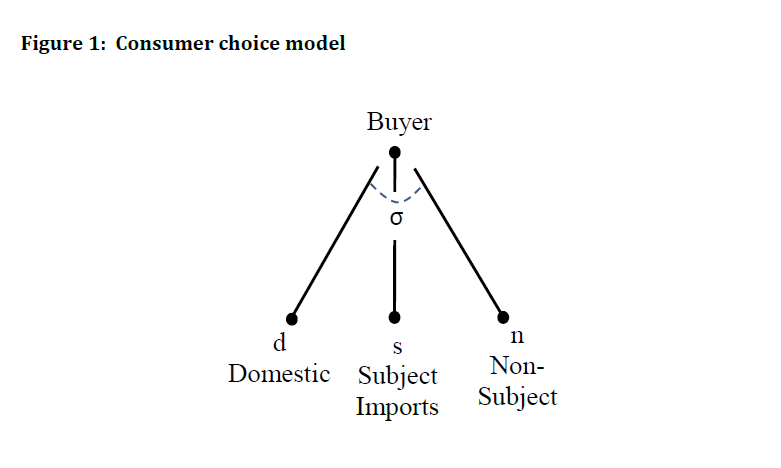
The model assumes that there are three varieties of products in the industry that are imperfect substitutes in demand. The three varieties are the domestic product, subject imports, and non-subject imports, denoted by the subscripts $d$ , $s$ , and $n$ . Subject imports are those directly affected by the change in trade policy (e.g., the imports experiencing the reduction in tariff rates), and non-subject imports are all other imports. For example, if the U.S. were to give duty free status to Pashminas from Bhutan, then Bhutanese Pashminas would be the subject foreign variety and Pashminas from India would be non-subject. All three varieties are imperfect substitutes and consumers substitute between the each variety at a constant rate ( $σ$ ). This term is called the “Armington elasticity.”[2] It is a key element in the model because it tells us how much sensitive consumers are to changes in the relative prices of each of the three varieties. Figure 1 presents a conceptual diagram of the model.

Figure 1 shows that consumers substitute between domestic product, subject imports, and non-subject imports, with an elasticity of substitution equal to sigma.

3. Model Derivation

Table 1 lists the data inputs and economic outcomes in the basic partial equilibrium model used to analyze trade policy.

Table 1: Elements of the Model of the Impact of Ad Valorem Tariffs on the Industry

Data Inputs	Economic Outcomes
Market Share of Domestic Producers	Change in the Price of Domestic Producers
Market Share of Subject Imports	Change in the Price of Subject Imports
Market Share of Non-Subject Imports	Change in the Price of Non-Subject Imports
Supply Elasticity for Domestic Producers	Change in the Industry Price Index
Supply Elasticity for Subject Imports	Change in the Quantity of Domestic Producers
Supply Elasticity for Non-Subject Imports	Change in the Quantity of Subject Imports
Elasticity of Substitution within the Industry	Change in the Quantity of Non-Subject Imports
Price Elasticity of Total Demand
Tariff Rates on Subject Imports

The consumer prices for the three varieties of products are $p_{d}$ , $p_{s}$ , and $p_{n}$ . The producer price of the domestic product is $p_{d}$ , while the producer prices of the two varieties of imports are equal to $\frac{p_{s}}{t_{s}}$ and $\frac{p_{n}}{t_{n}}$ . The trade cost factor $t_{s}$ is equal to one plus the ad valorem equivalent rate of the tariff and international transport costs on subject imports, and $t_{n}$ is equal to one plus the ad valorem equivalent rate of the tariff and international transport costs on non-subject imports. The model focuses on a single national market. Consumers in the market can be a combination of households and industrial users, depending on the industry analyzed. The market shares for the three varieties of products in the industry ( $m_{d}$ , $m_{s}$ , and $m_{n}$ ) sum to one.

Equations (1), (2), and (3) are supply curves for the three varieties of products in the industry.

$q_{d} = a_{d} (p_{d})^{ε_{d}}$ (1)

$q_{s} = a_{s} {(\frac{p_{s}}{t_{s}})}^{ε_{s}}$ (2)

$q_{n} = a_{n} {(\frac{p_{n}}{t_{n}})}^{ε_{n}}$ (3)

The parameters $ε_{d}$ , $ε_{s}$ , $ε_{n}$ are constant price elasticities of supply, and $a_{d}$ , $a_{s}$ , $a_{n}$ represent factors that shift the supply curves. The equations for the supply curves assume a specific form (in this case, they are log-linear), and they are tailored to the industry by fitting the supply shift parameters to industry data. The calibrated values of the supply shifters reflect a variety of factors, including the level of production capacity and input costs. The model assumes that there is perfect competition in product markets.[3]

Equation (4) represents total demand in the industry, $Q$ .

$Q = Y P^{- θ}$ (4)

The variable $P$ is a price index for the products of the industry in the U.S. market, and the variable $Y$ represents U.S. aggregate expenditure on the product if $P = 1$ . If readers prefer to use the natural sign of the price elasticity of demand, then (4) should be rewritten as

$Q = Y P^{θ}$ ( 4’ )

Armington (1969) demonstrates that the consumer demand for variety $i \in {1, n}$ is generated from solving the following utility maximization problem:

$\max U (q_{i}) = \sum {(b_{i} q_{i}^{\frac{σ - 1}{σ}})}^{\frac{σ}{1 - σ}} s . t . Y = \sum p_{i} q_{i}$

Equations (5), (6), and (7) are Constant Elasticity of Substitution (CES) demand curves for the three varieties of products.[4]

$q_{d} = Q b_{d}^{σ} {(\frac{p_{d}}{P})}^{- σ}$ (5)

$q_{s} = Q b_{s}^{σ} {(\frac{p_{s}}{P})}^{- σ}$ (6)

$q_{n} = Q b_{n}^{σ} {(\frac{p_{n}}{P})}^{- σ}$ (7)

The parameter $θ$ is the absolute value of the price elasticity of total demand in the industry.[5] The parameter $b_{d}$ , $b_{s}$ , and $b_{n}$ represent factors that shift the demand curves. The equations of the demand curves also assume specific functional forms (in this case, they are log linear in prices and the price index, and the price index has a CES functional form). These equations are also tailored to the industry by fitting the demand shift parameters to industry data. The calibrated values of the demand shifters reflect a variety of factors, including prices in other industries.

We use equations (1) through (7) to calculate the effect of the change in the tariff on subject imports. Equations (8) through (13) are log-linearized versions of equations (1) through (7). We have converted the original equations into percentage changes.[6] For every variable $v$ , we use the notation $\hat{v}$ to denote the percentage change $d v / v$ . In line with our partial equilibrium approach, we assume that the factors implicit in the supply and demand shift parameters ( $a_{d}$ , $a_{s}$ , $a_{n}$ , $b_{d}$ , $b_{s}$ , and $b_{n}$ ) do not change with the change in trade policy, so they do not appear as changes in equations (8) through (13). Likewise, we assume that there is no change in U.S. aggregate expenditure ( $\hat{Y}$ is equal to zero).

${\hat{q}}_{d} = ε_{d} {\hat{p}}_{d}$ (8)

${\hat{q}}_{s} = ε_{s} ({\hat{p}}_{s} - {\hat{t}}_{s})$ (9)

${\hat{q}}_{n} = ε_{n} {\hat{p}}_{n}$ (10)

${\hat{q}}_{d} = (σ - θ) \hat{P} - σ {\hat{p}}_{d}$ (11)

${\hat{q}}_{s} = (σ - θ) \hat{P} - σ {\hat{p}}_{s}$ (12)

${\hat{q}}_{n} = (σ - θ) \hat{P} - σ {\hat{p}}_{n}$ (13)

Equation (14) represents the percentage change in the industry’s overall price index $P$ . It is a market share-weighted average of the percentage changes in the consumer prices of the three varieties of products.

$\hat{P} = m_{d} {\hat{p}}_{d} + m_{s} {\hat{p}}_{s} + m_{n} {\hat{p}}_{n}$ (14)

The demand and supply shift parameters ( $a_{d}$ , $a_{s}$ , $a_{n}$ , $b_{d}$ , $b_{s}$ , and $b_{n}$ ) are implicitly reflected in the market shares in equation (14).

We assume that prices adjust to the policy changes to ensure that the market for each of the three varieties of products continues to clear. For this reason, the percentage change in quantity supplied is equal to the percentage change in the quantity demanded of each of the products. Equations (15) through (17) jointly determine the changes in the prices of the three varieties of products, based on equations (8) through (14). In the policy scenario that we consider, we assume that there are no changes in the trade costs on non-subject imports ( ${\hat{t}}_{n}$ is equal to zero).

$(σ - θ) (m_{d} {\hat{p}}_{d} + m_{s} {\hat{p}}_{s} + m_{n} {\hat{p}}_{n}) - σ {\hat{p}}_{d} = ε_{d} {\hat{p}}_{d}$ (15)

$(σ - θ) (m_{d} {\hat{p}}_{d} + m_{s} {\hat{p}}_{s} + m_{n} {\hat{p}}_{n}) - σ {\hat{p}}_{s} = ε_{s} ({\hat{p}}_{s} - {\hat{t}}_{s})$ (16)

$(σ - θ) (m_{d} {\hat{p}}_{d} + m_{s} {\hat{p}}_{s} + m_{n} {\hat{p}}_{n}) - σ {\hat{p}}_{n} = ε_{n} {\hat{p}}_{n}$ (17)

Finally, we solve equations (15), (16), and (17) for the percentage changes in the prices of the three varieties of products in the industry. The reduced-form solutions for the price changes are represented by equations (18), (19), and (20).

${\hat{p}}_{d} = {\hat{t}}_{s} \frac{m_{s} ε_{s} (σ - θ)}{(ε_{s} + σ) (ε_{d} + σ) (1 + \frac{m_{d} (θ - σ)}{ε_{d} + σ} + \frac{m_{s} (θ - σ)}{ε_{s} + σ} + \frac{m_{n} (θ - σ)}{ε_{n} + σ})}$ (18)

${\hat{p}}_{s} = {\hat{t}}_{s} \frac{ε_{s} (1 + \frac{m_{n} (θ - σ)}{ε_{n} + σ} + \frac{m_{d} (θ - σ)}{ε_{d} + σ})}{(ε_{s} + σ) (1 + \frac{m_{d} (θ - σ)}{ε_{d} + σ} + \frac{m_{s} (θ - σ)}{ε_{s} + σ} + \frac{m_{n} (θ - σ)}{ε_{n} + σ})}$ (19)

${\hat{p}}_{n} = {\hat{t}}_{s} \frac{m_{s} ε_{s} (σ - θ)}{(ε_{s} + σ) (ε_{n} + σ) (1 + \frac{m_{d} (θ - σ)}{ε_{d} + σ} + \frac{m_{s} (θ - σ)}{ε_{s} + σ} + \frac{m_{n} (θ - σ)}{ε_{n} + σ})}$ (20)

To solve for the percentage change in the industry’s overall price index, we substituted the price changes in equations (18), (19), and (20) into equation (14). To solve for the percentage changes in quantities, we substituted these price changes into equations (8), (9), and (10).

4. Data Inputs

One key input of the model is the total expenditures on the products of the industry in the U.S. market. The simplest way to approximate total expenditure is to calculate apparent consumption, defined as the total shipments of U.S. producers in the industry minus their exports plus U.S. imports. It is possible, but usually difficult, to estimate consumption based on data from expenditure surveys. The problem is that the categories in these surveys are often not defined narrowly enough for an industry or product-level analysis. The market shares for the different varieties of products ( $m_{d}$ , $m_{s}$ , or $m_{n}$ ) are equal to the values of domestic shipments, subject imports, or non-subject imports divided by total expenditures on the products of the industry.

A second key input is the elasticity of substitution among the products, $σ$ . This parameter value is often taken from estimates in the academic econometrics literature.[7] It may be possible to generate a new econometric estimate of this model parameter for the model if there are no estimates available in the literature.[8] One way to reflect uncertainty about the value of this parameter is to report the estimates of economic impacts for a range of potential parameter values rather than a single value.[9]

The parameter $θ$ is the absolute value of the price elasticity of total demand in the industry. This model parameter could also be estimated in a new econometric analysis or it could be borrowed from the literature. The appropriate value of this parameter depends on specific conditions in the industry. For example, if there were no products from outside of the industry that serve as substitutes for the products of the industry, then this price elasticity would be very small.

Likewise, the appropriate values for the supply elasticities ( $ε_{d}$ , $ε_{s}$ , and $ε_{n}$ ) depend on conditions in the industry. An extreme but useful simplification is to assume that these supply elasticities are infinite.[10] In this case, prices do not change in response to the policy change.

The simulation model is static, rather than dynamic. This means that it does not predict the speed of adjustment in prices and quantities after the policy change. Still, timing can be roughly incorporated into the model through the selection of the values of the elasticity parameters $-$ lower elasticities for an analysis of short-run effects and higher elasticities for a longer-run analysis $-$ though this is probably a poor substitute for an explicitly dynamic model.

5. Illustrative Application #1: Reductions in Ad Valorem Tariffs

In this section, we report several applications of the model. In our first example, we model a reduction in the import ad-valorem tariff applied to subject imports from 5 to 0 percent. Figure 2 illustrates the adjustments that result from the tariff change. When the tariff is removed, the supply of subject imports increases, and the market price of subject imports falls. Because the three varieties are substitutes, the decline in the market price of subject imports causes consumers to buy more of the subject imports in lieu of the other two varieties, and this is reflected as a reduction in demand for the domestic and non-subject varieties. The model predicts that removing a tariff on subject imports will result in a decline in the market price of all varieties, an increase in quantity demanded of subject imports, and a decrease in quantity demanded of the domestic product and non-subject imports.

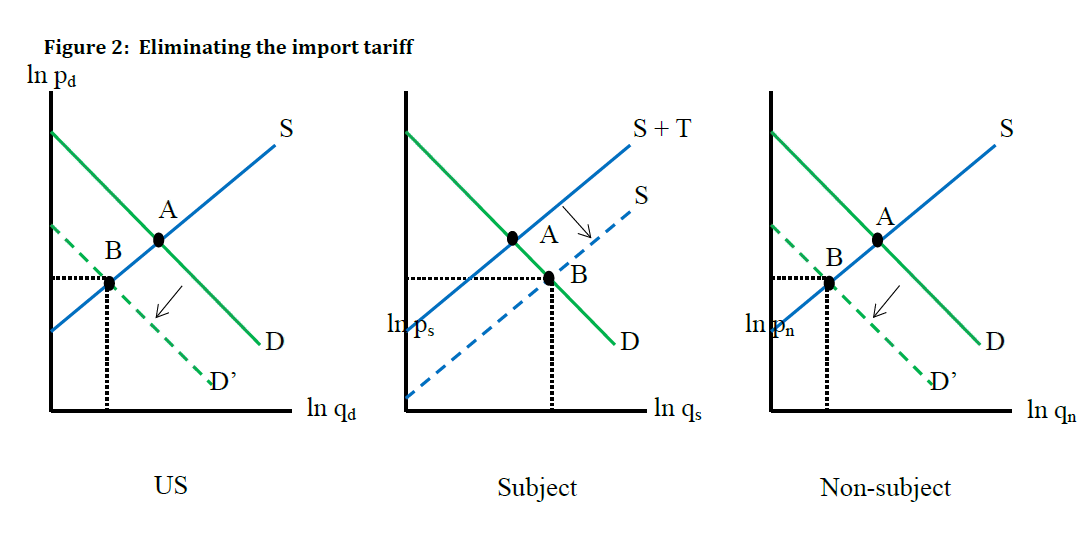
Title: Figure 2 shows the shifts in the demand and supply curves for the three products when the import tariff is eliminated.

Table 2 reports the estimated magnitudes of the changes in the prices of the three varieties of products, the industry’s overall price index, and the quantities of the products as a result of a reduction in the ad valorem tariff on subject imports from 5 to 0 percent. This implies a 4.76 percent reduction in $t_{s}$ (if there are no international transport costs in $t_{s}$ ). The table reports five different versions of the model with alternative assumptions about market shares and elasticity parameters.

Table 2: Reducing an Ad Valorem Tariff

	v1	v2	v3	v4	v5
Data Inputs
Market Share of Domestic Producers (percent)	33.33	70.00	33.33	33.33	33.33
Market Share of Subject Imports (percent)	33.33	10.00	33.33	33.33	33.33
Market Share of Non-Subject Imports (percent)	33.33	20.00	33.33	33.33	33.33
Supply Elasticity for Domestic Producers	1	1	5	1	1
Supply Elasticity for Subject Imports	10	10	10	10	10
Supply Elasticity for Non-Subject Imports	10	10	10	10	10
Elasticity of Substitution within the Industry	5	5	5	5	6
Price Elasticity of Total Industry Demand	1	1	1	0.5	1
Changes in Trade Policy
Initial Tariff Rate on Subject Imports (percent)	5.00	5.00	5.00	5.00	5.00
Revised Tariff Rate on Subject Imports (percent)	0.00	0.00	0.00	0.00	0.00
Percentage Changes in Prices
Change in the Price of the Domestic Product	-1.18	-0.47	-0.61	-1.44	-1.28
Change in the Price of Subject Imports	-3.64	-3.36	-3.58	-3.75	-3.54
Change in the Price of Non-Subject Imports	-0.47	-0.19	-0.41	-0.58	-0.56
Change in the Industry Price Index	-1.76	-0.70	-1.54	-1.92	-1.79
Percentage Changes in Quantities
Change in the Quantity of the Domestic Product	-1.18	-0.47	-3.07	-1.44	-1.28
Change in the Quantity of Subject Imports	11.17	14.01	11.78	10.10	12.26
Change in the Quantity of Non-Subject Imports	-4.70	-1.87	-4.10	-5.77	-5.60

In the first version of the model (column v1 in table 2), the tariff change reduces the price of subject imports by 3.64 percent and reduces the prices of the domestic product and non-subject imports by 1.18 and 0.47 percent. The industry’s overall price index falls 1.76 percent. The reduction in the tariff on subject imports increases the quantity of subject imports by 11.17 percent but reduces the quantity of domestic product and non-subject imports by 1.18 and 4.70 percent.

The remaining columns in the table report the sensitivity of these estimates to the data inputs of the model. Alternative v2 shows that, all else equal, a larger market share of domestic producers and a smaller market share of subject imports reduces the absolute magnitudes of all of the price and quantity changes except the increase in the quantity of subject imports, which is magnified.[11] Alternative v3 shows that greater supply elasticity of domestic producers (relative to the benchmark value in alternative v1) reduces the magnitude of the decline in the price of domestic producers but increases the decline in their quantity. Alternative v4 shows that a reduction in the price elasticity of total industry demand increases the decline in all of the prices and increases the decline in the quantity of the domestic product. Finally, alternative v5 shows that an increase in the elasticity of substitution (relative to the benchmark value) increases the percentage declines in prices of domestic products and non-subject imports and also increases the percentage declines in the quantities of these products.

6. Illustrative Application #2: Increase in an Import Quota

In our second example, we model an increase in a binding import quota. By binding we mean that equilibrium, consumers will purchase the full amount of subject imports allowed under the quota. Figure 3 illustrates the adjustments resulting from this policy change. The supply curve for subject imports is the line $\bar{a b B c}$ without any quota. With the initial quota in place, the supply curve is line $\bar{a b A S}$ . Buyers can purchase up to the quota amount. At that amount, the supply curve becomes perfectly inelastic and any increase in demand translates into an increase in the market price for subject imports with no further changes in quantity. When the quota is increased, the supply curve for subject imports becomes $\bar{a b B S'}$

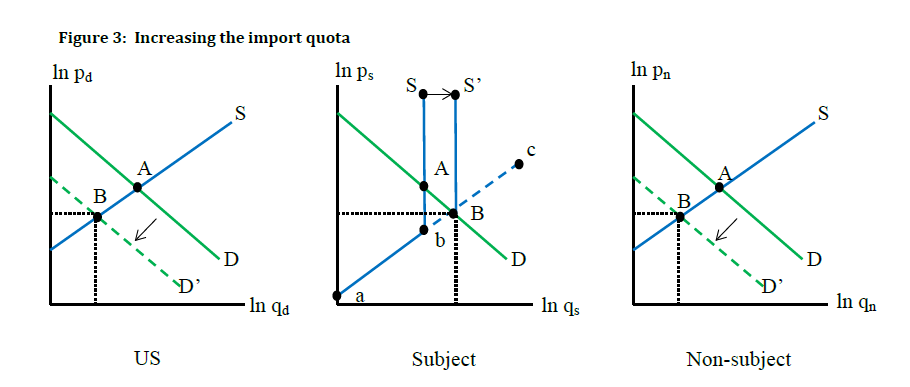
By binding we mean that equilibrium, consumers will purchase the full amount of subject imports allowed under the quota. Figure 3 illustrates the adjustments resulting from this policy change.

Given the demand for subject imports, the market price of subject imports falls. Because the three varieties (domestic, subject, and non-subject) are substitutes, when the price of subject imports falls, demand for the other two varieties declines. Consequently, the effects of increasing a binding import quota are a reduction in the market price of all varieties, an increase in the market share of subject imports, and a decline in the market shares of domestic and non-subject imports.

The derivation of the equations of the model in section 2 focuses on a change in an ad valorem tariff. We can also derive the equations for a change in the binding quota. In this case, ${\hat{q}}_{s}$ is an exogenous parameter in equation (12), and equation (9) drops from the model.[12] Equations (21), (22), and (23) quantify the resulting percentage changes in the prices of the three varieties, and equation (14) still defines the percentage change in the industry’s overall price index.

${\hat{p}}_{d} = {\hat{q}}_{s} (\frac{\frac{(θ - σ) m_{s}}{σ}}{(ε_{d} + σ) (1 + (\frac{(θ - σ) m_{d}}{ε_{d} + σ} + \frac{(θ - σ) m_{n}}{ε_{n} + σ} + \frac{(θ - σ) m_{s}}{σ}))})$ (21)

${\hat{p}}_{s} = {\hat{q}}_{s} (\frac{\frac{(σ - θ) m_{d}}{ε_{d} + σ} + \frac{(σ - θ) m_{n}}{ε_{n} + σ} - 1}{σ (1 + (\frac{(θ - σ) m_{d}}{ε_{d} + σ} + \frac{(θ - σ) m_{n}}{ε_{n} + σ} + \frac{(θ - σ) m_{s}}{σ}))})$ (22)

${\hat{p}}_{n} = {\hat{q}}_{s} (\frac{\frac{(θ - σ) m_{s}}{σ}}{(ε_{n} + σ) (1 + (\frac{(θ - σ) m_{d}}{ε_{d} + σ} + \frac{(θ - σ) m_{n}}{ε_{n} + σ} + \frac{(θ - σ) m_{s}}{σ}))})$ (24)

Table 3 reports the estimated price and quantify effects of a ten percent increase in the binding quota on subject imports, for the same five combinations of data inputs considered in table 2.

Table 3: Increasing a Binding Import Quota

	v1	v2	v3	v4	v5
Data Inputs
Market Share of Domestic Producers (percent)	33.33	70.00	33.33	33.33	33.33
Market Share of Subject Imports (percent)	33.33	10.00	33.33	33.33	33.33
Market Share of Non-Subject Imports (percent)	33.33	20.00	33.33	33.33	33.33
Supply Elasticity for Domestic Producers	1	1	5	1	1
Supply Elasticity for Subject Imports	10	10	10	10	10
Supply Elasticity for Non-Subject Imports	10	10	10	10	10
Elasticity of Substitution within the Industry	5	5	5	5	6
Price Elasticity of Total Industry Demand	1	1	1	0.5	1
Percentage Change in Binding Import Quota	10.00	10.00	10.00	10.00	10.00
Percentage Changes in Prices
Change in the Price of the Domestic Product	-1.05	-0.33	-0.52	-1.43	-1.04
Change in the Price of Subject Imports	-3.26	-2.40	-3.04	-3.71	-2.89
Change in the Price of Non-Subject Imports	-0.42	-0.13	-0.35	-0.57	-0.46
Change in the Industry Price Index	-1.58	-0.50	-1.30	-1.90	-1.46
Percentage Changes in Quantities
Change in the Quantity of the Domestic Product	-1.05	-0.33	-2.61	-1.43	-1.04
Change in the Quantity of Subject Imports	10.00	10.00	10.00	10.00	10.00
Change in the Quantity of Non-Subject Imports	-4.21	-1.33	-3.48	-5.71	-4.57

Like the reduction in a tariff on subject imports, the increase in a binding quota on subject imports reduces the price of subject imports and reduces the prices of the domestic product and non-subject imports (column v1 in table 2). The increase in the quota increases the quantity of subject imports and reduces the quantity of domestic product and non-subject imports.

Again, the remaining columns of the table report the sensitivity of the magnitude of the percentage changes to the data inputs. Alternative v2 shows that, all else equal, a larger market share of domestic producers and a smaller market share of subject imports reduces the absolute magnitudes of all of the quantity and price changes (except the percentage change in the quantity of subject imports, which is set by the increase in the quota). Alternative v3 shows that greater supply elasticity of domestic producers (relative to the benchmark value in alternative v1) reduces the magnitude of the decline in the price of domestic producers but increases the decline in their quantity of their domestic shipments. Alternative v4 shows that a reduction in the price elasticity of total industry demand increases the decline in all of the prices and increases the decline in the quantity of the domestic product. Finally, alternative v5 shows that an increase in the elasticity of substitution (relative to the benchmark value) reduces the declines in the price and quantity of domestic products.

7. Non-Linear Versions of the Models

We reran the simulations using the exact non-linear functional forms in equations (1) through (7), which are log-linear, as well as the CES price index for the industry, which is not log-linear.

To solve the non-linear version of the model, one uses an iterative algorithm to find the set of prices that ensures that quantity supplied equals quantity demanded in all markets simultaneously. Fetzer (2005) describes the derivation of the following set of equations.

${(\frac{p_{i}}{t_{i}})}^{ε_{i}} = \frac{P^{σ - θ}}{p_{i}^{σ}} f o r a l l i \in d o m, s u b j, n o n - s u b j$

We solve the model in Excel by via an iterative algorithm that solves the following sum of squared errors (SSE) minimization problem:

$\min_{p_{i}} S S E = min_{p_{i}} \sum {({(\frac{p_{i}}{t_{i}})}^{ε_{i}} - \frac{P^{σ - θ}}{p_{i}^{σ}})}^{2}$

Table 4 is a side-by-side comparison the simulation results for the first two versions of the reduction in an ad valorem tariff, using the log-linearized model as in Table 2 and then using the exact non-linear model. The estimated price and quantity effects are amplified (the percentage changes are larger in absolute value) using the non-linear model, but the differences are small, reflecting the fact that the model is almost completely log-linear before any linearization.

Table 4: Comparison of Models for a Reduction in an Ad Valorem Tariff

	Log-Linearized v1	Non-Linear v1	Log-Linearized v2	Non-Linear v2
Data Inputs
Market Share of Domestic Producers (percent)	33.33	33.33	70.00	70.00
Market Share of Subject Imports (percent)	33.33	33.33	10.00	10.00
Market Share of Non-Subject Imports (percent)	33.33	33.33	20.00	20.00
Supply Elasticity for Domestic Producers	1	1	1	1
Supply Elasticity for Subject Imports	10	10	10	10
Supply Elasticity for Non-Subject Imports	10	10	10	10
Elasticity of Substitution within the Industry	5	5	5	5
Price Elasticity of Total Industry Demand	1	1	1	1
Changes in Trade Policy
Initial Tariff Rate on Subject Imports (percent)	5.00	5.00	5.00	5.00
Revised Tariff Rate on Subject Imports (percent)	0.00	0.00	0.00	0.00
Percentage Changes in Prices
Change in the Price of the Domestic Product	-1.18	-1.24	-0.47	-0.50
Change in the Price of Subject Imports	-3.64	-3.68	-3.36	-3.40
Change in the Price of Non-Subject Imports	-0.47	-0.50	-0.19	-0.20
Change in the Industry Price Index	-1.76	-1.85	-0.70	-0.75
Percentage Changes in Quantities
Change in the Quantity of the Domestic Product	-1.18	-1.24	-0.47	-0.50
Change in the Quantity of Subject Imports	11.17	11.35	14.01	14.35
Change in the Quantity of Non-Subject Imports	-4.70	-4.97	-1.87	-2.01

Table 5 is a side-by-side comparison the simulation results for the first two versions of the increase in a binding quota, using the log-linearized model as in Table 3 and then using the exact non-linear model. The estimated price and quantity effects are dampened (the percentage changes are smaller in absolute value) using the non-linear model, but the differences are very small.

Table 5: Comparison of Models for an Increase in a Binding Import Quota

	Log-Linear v1	Non-Linear v1	Log-Linear v2	Non-Linear v2
Data Inputs
Market Share of Domestic Producers (percent)	33.33	33.33	70.00	70.00
Market Share of Subject Imports (percent)	33.33	33.33	10.00	10.00
Market Share of Non-Subject Imports (percent)	33.33	33.33	20.00	20.00
Supply Elasticity for Domestic Producers	1	1	1	1
Supply Elasticity for Subject Imports	10	10	10	10
Supply Elasticity for Non-Subject Imports	10	10	10	10
Elasticity of Substitution within the Industry	5	5	5	5
Price Elasticity of Total Industry Demand	-1	-1	-1	-1
Percentage Change in Binding Import Quota	10.00	10.00	10.00	10.00
Percentage Changes in Prices
Change in the Price of the Domestic Product	-1.05	-1.04	-0.33	-0.33
Change in the Price of Subject Imports	-3.26	-3.11	-2.40	-2.28
Change in the Price of Non-Subject Imports	-0.42	-0.42	-0.13	-0.13
Change in the Industry Price Index	-1.58	-1.55	-0.50	-0.49
Percentage Changes in Quantities
Change in the Quantity of the Domestic Product	-1.05	-1.04	-0.33	-0.33
Change in the Quantity of Subject Imports	10.00	10.00	10.00	10.00
Change in the Quantity of Non-Subject Imports	-4.21	-4.16	-1.33	-1.32

These examples suggest that it does not really matter whether the effects are calculated using a log-linearized model or the exact non-linear model. The log-linearized model is easier to implement, as simple cell formulas in Excel, but the non-linear model is also pretty straightforward to implement using a non-linear solver.

8. Conclusion

As we noted in the Introduction, there are many advantages to using a simpler modeling framework when analyzing the effects of trade policy changes that are narrowly targeting a specific industry. The model can provide quantitative estimates based on limited data inputs. It is easy to create, modify, and run.[13] The model is calibrated to the details the industry. For these reasons, industry-specific models can be very useful as a first cut analysis, prior to more detailed economic modeling, or as a test kitchen for experimentally adding new complexities into trade policy analysis.

The basic partial equilibrium model can be extended in many directions to better fit the economic complexities of the industry analyzed.[14] For example, the beef model in Hallren and Opanasets (2016) includes vertically integrated production and trade in intermediate products. The household appliances model in Hallren and Riker (2017) includes sub-national regions within the United States. The models of architectural, engineering, and legal services in Khachaturian and Riker (2016, 2017) and Barbe, Chambers, Khachaturian and Riker (2017) include multiple modes of international supply of the services (e.g., cross-border exports and foreign affiliate sales) and fixed costs of trade, as well as ad valorem tariffs. The equations and data requirements of these extended models are more elaborate, but the principles of model building are the same.

References

Armington, Paul S. (1969): “A Theory of Demand for Products Distinguished by Place of Production.” Staff Papers (International Monetary Fund) 16 (1): 159-78.

Barbe, Andre, Arthur Chambers, Tamar Khachaturian and David Riker (2017): “Modeling Trade in Services: Multiple Modes, Barriers to Trade, and Data Limitations.” USITC Economics Working Paper No. 2017-04-B.

Fetzer, James J. (2005): “A Partial Equilibrium Approach of Modeling Vertical Linkages in the U.S. Flat Rolled Steel Market.” USITC Economics Working Paper No. 2005-01-A.

Hallren, Ross and Alexandra Opanasets (2016): “Whence the Beef? The Effects of Repealing Mandatory Country of Origin Labeling (COOL) using a Vertically Integrated Armington Model with Monte Carlo Simulation.” USITC Economics Working Paper No. 2016-09-A.

Hallren, Ross and David Riker (2017): “A U.S. Regional Model of Import Competition and Jobs.” USITC Economics Working Paper No. 2017-2-A.

Hertel, Thomas, David Hummel, Maros Ivanic, and Roman Keeney (2007): “How Confident Can We Be of CGE-Based Assessments of Free Trade Agreements.” Economic Modeling 24 (4): 611-635.

Khachaturian, Tamar and David Riker (2016): “A Multi-Mode Partial Equilibrium Model of Trade in Professional Services.” USITC Economics Working Paper No. 2016-10-A.

Khachaturian, Tamar and David Riker (2017): “The Impact of Liberalizing International Trade in Professional Services.” Journal of International Commerce and Economics, May 2017.

Appendix: Simulations Using a Non-Linear Version of the Models

Table A1: Non-Linear Model of a Reduction in an Ad Valorem Tariffs

	v1	v2	v3	v4	v5
Data Inputs
Market Share of Domestic Producers (percent)	33.33	70.00	33.33	33.33	33.33
Market Share of Subject Imports (percent)	33.33	10.00	33.33	33.33	33.33
Market Share of Non-Subject Imports (percent)	33.33	20.00	33.33	33.33	33.33
Supply Elasticity for Domestic Producers	1	1	5	1	1
Supply Elasticity for Subject Imports	10	10	10	10	10
Supply Elasticity for Non-Subject Imports	10	10	10	10	10
Elasticity of Substitution within the Industry	5	5	5	5	6
Price Elasticity of Total Industry Demand	-1	-1	-1	-0.5	-1
Changes in Trade Policy
Initial Tariff Rate on Subject Imports (percent)	5.00	5.00	5.00	5.00	5.00
Revised Tariff Rate on Subject Imports (percent)	0.00	0.00	0.00	0.00	0.00
Percentage Changes in Prices
Change in the Price of the Domestic Product	-1.24	-0.50	-0.65	-1.52	-1.35
Change in the Price of Subject Imports	-3.68	-3.40	-3.62	-3.79	-3.58
Change in the Price of Non-Subject Imports	-0.50	-0.20	-0.44	-0.61	-0.59
Change in the Industry Price Index	-1.85	-0.75	-1.62	-2.01	-1.89
Percentage Changes in Quantities
Change in the Quantity of the Domestic Product	-1.24	-0.50	-3.26	-1.52	-1.35
Change in the Quantity of Subject Imports	11.35	14.35	11.97	10.21	12.41
Change in the Quantity of Non-Subject Imports	-4.97	-2.01	-4.35	-6.09	-5.95

Table A2: Non-Linear Model of an Increase in a Binding Import Quota

	v1	v2	v3	v4	v5
Data Inputs
Market Share of Domestic Producers (percent)	33.33	70.00	33.33	33.33	33.33
Market Share of Subject Imports (percent)	33.33	10.00	33.33	33.33	33.33
Market Share of Non-Subject Imports (percent)	33.33	20.00	33.33	33.33	33.33
Supply Elasticity for Domestic Producers	1	1	5	1	1
Supply Elasticity for Subject Imports	10	10	10	10	10
Supply Elasticity for Non-Subject Imports	10	10	10	10	10
Elasticity of Substitution within the Industry	5	5	5	5	6
Price Elasticity of Total Industry Demand	-1	-1	-1	-0.5	-1
Percentage Change in Binding Import Quota	10.00	10.00	10.00	10.00	10.00
Percentage Changes in Prices
Change in the Price of the Domestic Product	-1.04	-0.33	-0.52	-1.42	-1.03
Change in the Price of Subject Imports	-3.11	-2.28	-2.90	-3.55	-2.76
Change in the Price of Non-Subject Imports	-0.42	-0.13	-0.34	-0.57	-0.45
Change in the Industry Price Index	-1.55	-0.49	-1.29	-1.89	-1.44
Percentage Changes in Quantities
Change in the Quantity of the Domestic Product	-1.04	-0.33	-2.58	-1.42	-1.03
Change in the Quantity of Subject Imports	10.00	10.00	10.00	10.00	10.00
Change in the Quantity of Non-Subject Imports	-4.16	-1.32	-3.44	-5.69	-4.53

[1] An ad valorem tariff is a fixed percentage of the value of the imports rather than a specific dollar amount per unit of quantity. The model can also be modified to analyze specific tariffs.

[2] The Armington elasticity has the following qualitative values. If σ = 0, the domestic and foreign varieties are perfect complements. If σ = 1, then preferences are Cobb-Douglas and domestic and foreign varieties are consumed with fixed expenditure shares. If σ > 1, then domestic and foreign varieties are substitutes and in this case a fall in the price of good j, ceteris paribus, improves its competitiveness and thus its market share. As is well established, if the Armington elasticity is less than or equal to 1, then a fall in the price of a goods from country A results in a decline in country A’s market share. Armington (1969).

[3] It is not difficult to extend the model to include imperfect competition, but in this case the producers have cost curves but not supply curves. The models in Khachaturian and Riker (2016) and Barbe, Chambers, Khachaturian and Riker (2017) include monopolistic competition, for example.

[4] The model assumes that the CES preferences for the three varieties of products are non-nested.

[5] Technically, it is the absolute value of the price elasticity of the CES composite of the products of the industry. It could also be interpreted as a constant elasticity of substitution between the products of different industries if the share of the specific industry is close to zero.

[6] Specifically we have differentiated equations (1) through (6) with respect to the prices, quantities, and tariff rates.

[7] For example, Hertel, Hummel, Ivanic, and Keeney (2007) reports estimates of this elasticity at a fairly disaggregated industry level.

[8] For example, this is the approach in the analysis of household appliances in Hallren and Riker (2017).

[9] Another more elaborate way to reflect the uncertainty in the parameter values is to run Monte Carlo simulations over a distribution of potential values, as in Hallren and Opanasets (2016).

[10] For example, Hallren and Opanasets (2016) adopt this assumption for the upstream products in their model.

[11] A smaller tariff reduction would also reduce the absolute magnitudes of all of the quantity and price changes.

[12] Exogeneity means that the quantity imported is not determined by market prices. It is set by trade policy.

[13] The model used in the illustrative applications in tables 2 and 3 is run in an Excel worksheet with simple cell formulas.

[14] The following examples are USITC research papers that are available at httpss://www.usitc.gov/research_and_analysis/staff_products.htm.