THE DYNAMIC GRAVITY DATASET: 1948–2016
AUTHORS
Tamara Gurevich
Peter Herman
DATASET CONTRIBUTORS
Nabil Abbyad
Meryem Demirkaya
Austin Drenski
Tamara Gurevich
Peter Herman
Jeffrey Horowitz
Grace Kenneally
ECONOMICS WORKING PAPER SERIES
Working Paper 2018–02–A
U.S. INTERNATIONAL TRADE COMMISSION
500 E Street SW
Washington, DC 20436
February 2018
Office of Economics working papers are the result of ongoing professional research of USITC Staff and are solely meant to represent the opinions and professional research of individual authors. These papers are not meant to represent in any way the views of the U.S. International Trade Commission or any of its individual Commissioners. Working papers are circulated to promote the active exchange of ideas between USITC Staff and recognized experts outside the USITC and to promote professional development of Office Staff by encouraging outside professional critique of staff research. Please address all correspondence to Tamara.Gurevich@usitc.gov or Peter.Herman@usitc.gov.
The Dynamic Gravity Dataset: 1948–2016
Tamara Gurevich, Peter Herman
Office of Economics Working Paper 2018–02–A
February 2018
Abstract
The estimation of gravity models of international trade extensively relies on the availability of unilateral and bilateral, country pair measures of theoretical determinants of trade. Existing datasets provide a wealth of information, but often come short in terms of temporal and other forms of variation. This paper presents a recently developed Dynamic Gravity dataset that improves upon existing gravity datasets by including additional variables of interest and featuring greater variation for use in econometric analysis. We describe the dataset and highlight the key differences between our Dynamic Gravity dataset and the datasets often used by researchers previously. Analytical comparisons are included that demonstrate important similarities and differences through summary statistics and estimates of sample gravity models using the Dynamic Gravity dataset and two alternative data sources: the CEPII gravity database constructed by Head et al. (2010) and the Rose (2004) dataset. We find that the Dynamic Gravity dataset is nearly indistinguishable from the other sources and produces results consistent with international trade theory. However, in some cases, it produces results that are qualitatively similar but quantitatively different from the others, which we take as support that our attempts to improve on past datasets have succeeded.
Tamara Gurevich, Research Division, Office of Economics, USITC
tamara.gurevich@usitc.gov
Peter Herman, Research Division, Office of Economics, USITC
peter.herman@usitc.gov
Modern international trade research relies heavily on the use of gravity models of trade, which provide a powerful tool for explaining patterns of bilateral trade. Gravity data that details country characteristics and the relationships between trading partners is a critical input to this type of analysis. Importantly, these variables are used to measure or control for the effects of a wide collection of trade determinants such as trade facilitation policies, geographic barriers, and cultural influences that affect trade patterns between partners.1 The CEPII gravity dataset, currently the most prominent source of gravity trade data, has been used in nearly 650 research projects citing Head et al. (2010).2
In this paper, we describe a new gravity dataset that improves upon existing resources by providing gravity data that incorporates and emphasizes four things. First, it has been constructed to reflect the dynamic nature of the globe by closely following the ways in which countries and borders have changed between 1948 and 2016. This approach has culminated in a larger set of countries than available in other gravity resources as well as the ability to track their potential emergence or dissolution over time. Second, we have increased the time and magnitude of variation within several types of variables, which will improve the ability of researchers to identify relationships in econometric work. Third, we have developed concordances to new types of data series and included them as a part of the Dynamic Gravity dataset. These new variables include, for example, new measures of economic and political stability, geographical features, and macroeconomic indicators. Finally, we have attempted to make the construction of the dataset as transparent as possible so that users are never left with questions as to where data originated or how it was modified.
While existing gravity datasets are popular and widely used in gravity trade research, they exhibit some limitations.
Despite its frequent usage, the Rose (2004) dataset was developed for a particular research question and was not intended to be a widely used, general gravity resource. As a result, it has not experienced regular updates, its coverage ends in 1999, and it features a relatively limited set of 177 countries. Nonetheless, the dataset includes a wealth of country-specific and bilateral information that has made it a reliable source for gravity data in the past. This information includes GDP statistics, geographic characteristics, joint membership in trade agreements, language and colonial relationships, and numerous other variables that are mainstays of gravity modeling.
The dataset provided by Head et al. (2010) and made available through CEPII represents a collection of gravity variables for 224 countries.3 Until recently, the CEPII gravity dataset spanned the period between 1948 and 2006. Their gravity variables include a number of demographic, socio-economic, cultural, and trade-specific measures. Gurevich et al. (2017) updated the existing variables for the years 2007–2015 in January 2017. CEPII has since released a more comprehensive update in April 2017, extending the time frame to 2015 and adding some new variables. However, both the original CEPII gravity dataset and the two updates exhibit several limitations.
First, the set of countries is static and does not reflect the emergence or dissolution of many countries. For example, in records for 2015, the CEPII dataset includes identifiers and data for Yugoslavia but not Serbia, Montenegro, or Kosovo, which had all been independent and reporting trade for many years by 2015. While including the countries that no longer exist may not present problems when matching gravity variables with trade data, excluding the countries that have emerged more recently does. Importantly, these omissions may lead to biased estimates of the effects of particular gravity measures on trade flows given that they appear to be systematically connected to recently independent or geographically small nations.
The second limitation is that many of the CEPII gravity variables lack meaningful variation over time or with respect to magnitude. For example, CEPII’s conflict variable is completely static. It captures whether a country pair has ever been involved in a war but does not provide any indication as to whether the war was recent or occurred in the distant past.4 Because active or recent conflicts are much more likely to influence trade than historic conflicts, capturing time variation in conflict variables should increase their value significantly. Furthermore, the effect that a conflict might have on trade flows between countries may depend on the severity of the particular conflict. Again, the zero-one nature of CEPII’s variable may result in poor identification of the effects of conflicts compared to a data series that differentiates between levels of conflict.
To address many of these limitations present in other gravity datasets, we have constructed an all new gravity dataset that offers several advantages over other gravity sources. In addition to providing most of the same gravity variables that researchers have become accustomed to using, it improves upon many of these variables by emphasizing time and magnitude variation and transparency to the best extent possible. The dataset is composed of several dozen unilateral and bilateral variables for 285 countries and territories in existence between the years 1948 and 2016. These include an extensive set of macroeconomic indicators, geographic characteristics, trade facilitation variables, cultural variables, and measures of institutional stability, selected based on international trade theory and traditional gravity modeling methods.
In building this dataset, special attention was paid to the dynamic nature of the data, ensuring that the data recorded for each year accurately match the world in that year and that variables appropriately change over time to the greatest extent possible. For example, we have carefully traced the emergence and dissolution of countries over time, updating related variables each time a country or independent territory enters or exits the sample. Improvements upon this time variation allow for more accurate analysis of trade over time. We have also included within-country records in which countries are paired with themselves and bilateral variables reflect barriers to domestic commerce such as the average distance between major domestic markets. This inclusion will allow researchers to work with domestic production, consumption, or trade in addition to international trade. Importantly, the construction of the variables has been made as transparent as possible and includes extensive documentation describing data sources, construction procedures, and any assumptions employed in the creation of variables. Please see Gurevich et al. (2018) for these technical details. This technical documentation is available at gravity.usitc.gov.
The remainder of this paper proceeds as follows. Section 2 briefly describes the dataset, definitions, assumptions, and coding rules used in data collection and processing. Section 3 compares our dataset to some other commonly used gravity datasets and juxtaposes descriptive statistics for each. Section 4 presents results of some standard gravity model estimations using this gravity dataset as well as the other comparable sources of gravity data. Finally, section 5 concludes.
The Dynamic Gravity dataset includes an extensive set of macroeconomic indicators, geographic characteristics, trade facilitation variables, cultural variables, and measures of institutional stability for 285 countries and territories. From this list, we have created records for all pairs of all countries in existence each year. Additionally, the dataset includes records wherein countries are paired with themselves, allowing researchers to estimate the effects of various gravity variables and trade policies on domestic trade.
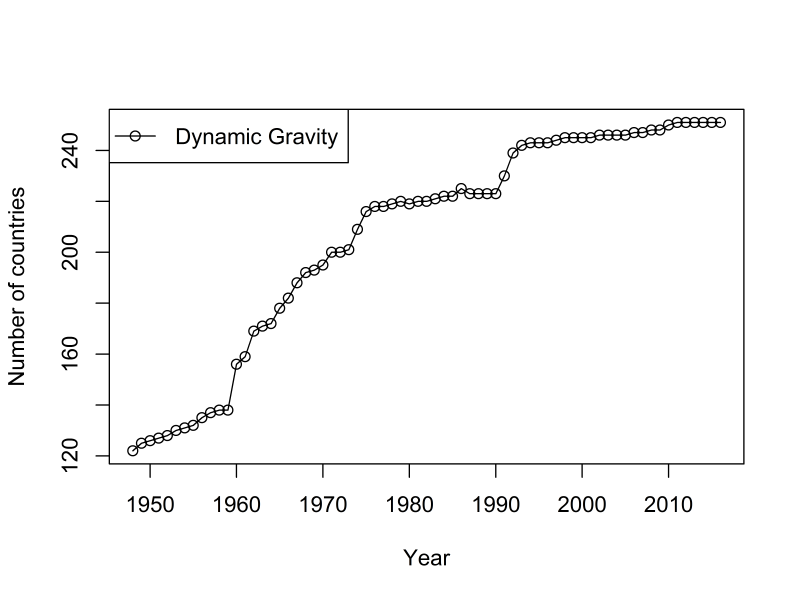
The dataset spans the years 1948–2016 and includes information on 285 countries and territories, some of which exist only for a subset of covered years. We first identified countries and territories to be included based on their official recognition by the WTO and United Nations as well as the presence of reported trade flows in the UN Comtrade database.5 For example, there are 122 countries and territories in 1948 and 251 countries and territories in 2016. Major growth in the number of countries and independent territories occurs first in the late 1950s through early 1970s as African countries gain independence from their colonial hegemons. A second expansion occurs in the 1990s as Southern- and Eastern-European countries—predominantly in the Soviet bloc—split into independent nations. One of the largest contributions of our data relative to existing datasets is this geographic and time variation we have introduced and placed at the center of much of the data.
Each record within the dataset is identified on the level of country pair and year. Throughout, the terminology “origin” and “destination” is used to differentiate between the two countries in each pair.6 Within each year, there are two records per country pair so that each country appears as both the origin and destination country within each pair and year. This results in nearly 3.1 million unique records ranging from 14,884 records and 122 country pairs in 1948 to 63,001 records and 251 country pairs in 2016. Figure 1 fully depicts the growth in the number of countries over the sample period.
The Dynamic Gravity dataset includes two different country-identifying codes. The first, ISO3-alpha, is the most commonly used identifier in trade and gravity datasets.7 We include this standard coding to allow for easier matching of our data with other data sources. However, even though country characteristics change over time, ISO3 codes do not always reflect these changes. Thus, we created an additional identifying variable, dynamic_code, that keeps track of countries that split, merge, or otherwise alter their borders but do not receive a new ISO code. While constructing the data, we identified fourteen countries with this issue.8 While the ISO3 code is useful when merging gravity data with conventional trade data, the dynamic_code is informative of changes in country borders and composition.
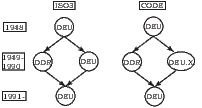
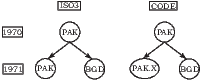
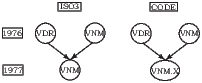
Figure 2 illustrates the differences between ISO3 and dynamic_code, using three possible scenarios as examples. In the first scenario, a country splits into two new countries—each featuring different macroeconomic, geographic, etc. characteristics than the parent country—and then reunites to re-form the original parent country. In the second scenario a country splits into two countries that do not reunite. In the last scenario two separate countries unite into one.
The left-most panel of figure 2 illustrates the split and reunification of East and West Germany. When Germany split in 1949, West Germany continued using ISO3 code “DEU” previously assigned to Germany while East Germany received a new code, “DDR”, assigned to it by the International Organization for Standardization. When the two countries reunited in 1991, ISO3 code “DEU” was transferred to the “new” unified Germany. However, West Germany and unified Germany feature different country characteristics such as contiguity, area, and population. Therefore, we indicate the changes in country characteristics by assigning West Germany a modified dynamic_code “DEU.X”.
The middle panel of figure 2 shows a second reason why ISO3 and dynamic_code may differ. Following Bangladesh’s split from Pakistan in 1971, Bangladesh receives a new ISO3 code, “BGD”, assigned to it by the International Organization for Standardization. As a result of this split, Pakistan lost nearly 16% of its land area and a common border with Myanmar. However, as before the split, it is still identified using ISO3 code “PAK”. We introduce a new dynamic_code, “PAK.X” to better indicate that characteristics of the “new” Pakistan often differ from the “old” Pakistan.
Finally, the last case, illustrated by the right panel of figure 2, demonstrates the coding of Vietnam following the post-war unification. Prior to 1977, North Vietnam is identified by ISO3 code “VDR” and South Vietnam is identified by ISO3 code “VNM”. Following the unification of the two countries, unified Vietnam inherits the ISO3 code of South Vietnam. To more clearly indicate that the new Vietnam is a combination of North and South Vietnam, we create dynamic_code “VNM.X” for the new country.
We have made available a wide array of macroeconomic indicators. Traditionally used variables include population, GDP, and GDP per capita, reported both in real and nominal terms for greater flexibility. Furthermore, we have included two additional variables that have not previously been a part of gravity datasets—real and nominal values of the capital stock—that may be of use to researchers as controls for the production capacity of countries, for example.
We have based these series on two sources: the Penn World Tables (PWT) and the World Bank’s World Development Indicators (WDI). Our objective was to provide the most thorough coverage possible over time and across countries.9 Given the slightly different methodologies used by the two sources, the inclusion both allows researchers to choose between the advantages offered by each. For example, PWT data is likely better suited for cross-country comparisons in a single a year while WDI data may be more appropriate for single-country comparisons over time. Together, the series cover about 10,000 country-years spanning the period between 1950 and 2016. Figure 6 shows the percent of countries in our dataset that are covered by the PWT and the WDI in each year.
For each country and territory in our dataset, we identify its latitude, longitude, geographic region, and whether it is an island or landlocked. Many of these variables have not been previously included in gravity datasets. For example, indicators for landlocked and island countries—illustrated in figure 7—can be used to better inform research related to land- or water-borne shipping. We also create a contiguity indicator for country pairs that share a common land border.
Each of the variables is carefully tracked over time and changes as countries and territories change their geographic characteristics. For example, the separation of Sudan into Sudan and South Sudan in 2011 results in changes in contiguity for Sudan itself as well as all countries that used to border it prior to the split. Ethiopia, Kenya, Uganda, Democratic Republic of the Congo, and Central African Republic all gain a new neighbor—South Sudan—while Kenya, Uganda, and Democratic Republic of the Congo also lose a neighbor—Sudan.
We calculate a greater circle distance between countries. This distance is weighted by population and location of large cities in each country to adjust for the economic center of gravity rather than simply using distance between the capitals or the geographic centers of two countries. This adjustment takes into account potentially large geographic area of many countries and recognizes that economic activity and trade usually do not occur only in a geographic center of a country or in its capital.
We create a set of unilateral and bilateral trade facilitation variables covering country membership in trade organizations and economic unions, such as the World Trade Organization and the European Union, as well as all preferential trade agreements recognized by the WTO (WTO, 2017a). We further subdivide the trade agreements into several categories including customs unions (CU), economic integration agreements (EIA), free trade agreements (FTA), and partial scope agreements (PSA). Figure 8 shows the relative frequency of country pairs belonging to trade agreements by type.10 Additionally, unlike previous gravity datasets, we separately identify trade agreements covering goods and those covering services. To illustrate, figure 9 depicts the relative frequency of country pairs belonging to trade agreements that do and do not cover services over time.
At the time of writing, the WTO recognized 484 trade agreements, including both active and inactive agreements.11 For these agreements, the WTO provides information on the original signatory members, the current signatories, the date an agreement went into force and, where applicable, the inactivity date. In several cases, we have supplemented the WTO RTA database with additional information on the timing of the entry and exit of countries that either joined or exited the agreement after it first went into force, which the WTO’s database does not always report. We have identified 48 such trade agreements, investigated their history, and amended the signatory list to reflect the changes. In doing so, we believe we have created the most comprehensive, accurate, and dynamic collection of variables reflecting trade agreements available as a part of a gravity dataset.
The set of cultural variables is designed to capture common cultural characteristics of country pairs. This set includes a number of colonial relationship indicators and an indicator for at least one common language shared by some portion of the population of the two countries or territories.
The language data is based on the CIA World Factbook.12 The World Factbook lists all languages spoken by as little as 1% of the population of each country. Using this list, we create an indicator based on the presence of at least one common language spoken in both countries.
The data on colonial relationships is derived from the Correlates of War Project (CoW) Colonial History dataset.13 In addition to concording the largely incompatible ISO3 and CoW country identifiers, we have supplemented the data to include colonial relationships that are not covered by the CoW. These additional data include colonies that have gained independence prior to 1816, the first year in CoW data, and those that are still colonies or have gained independence after 1997, the last year in CoW data.
The Dynamic Gravity dataset includes measures of institutional stability that may affect trade.
The first of these data series is a popular measure of political stability adopted from the Polity IV Project.14 The measure describes the stability of each country’s government and covers the majority of the world for the years 1948–2015, with some exceptions of countries during and following periods of conflict.15
The second set of institutional variables reflects aspects of geopolitical conflicts such as war. This data is derived from the Correlates of War (CoW) Project and covers the years 1948–2010.16 Not only does this dataset allow for the identification of concurrent conflicts within each year of the data, it permits differentiation between five varying severities of hostility ranging from “no militarized action taken” to “complete war”. The frequency and distribution of these indicators are depicted in 10.
The final set of institutional variables is derived from the Threat and Imposition of Economic Sanctions dataset created by Morgan et al. (2014).17 This dataset lists all sanctions threatened and/or imposed by individual countries and groups of countries through international institutions such as the United Nations and the European Union. We first create binary identifiers for whether a country has threatened or imposed sanctions against another country. This is then extended to additional indicators specifying whether the sanctions threatened or imposed are specific to trade. The frequency of these sanctions is plotted in figure 11.
In designing and constructing the Dynamic Gravity dataset, we have sought to improve upon key aspects of commonly used gravity datasets while maintaining the important features that researchers have come to expect from gravity resources. The remainder of the paper focuses on a collection of comparisons that highlight the similarities between the Dynamic Gravity dataset and two such alternate sources of gravity variables: the “CEPII” dataset constructed by Head et al. (2010) and the “Rose” dataset constructed by Rose (2004).
One such critical difference is the set of countries included in each dataset. Figure 12 compares the number of countries covered by the three datasets. As highlighted before, the Rose dataset features the most limited set of countries. In early years, the CEPII dataset features more countries than the Dynamic Gravity dataset. However, it is important to note that this difference is primarily a result of the static nature of the CEPII dataset and the inclusion of nonexistent countries in many years. The countries present only in the CEPII data are typically ones such as Russia and other Soviet bloc countries, which are included in the data in all years despite not existing between 1948 and 1991. In later years, when all these newly emerged countries are included, the Dynamic Gravity dataset features a greater number of countries.
Distance is one of the most commonly used gravity controls. Figure 13 compares the population-weighted distances as reported in the Dynamic Gravity dataset and in the CEPII dataset.18 We selected 2005 as the comparison year because this is the base year used in the CEPII dataset and compare only distances between countries available in both datasets. As evident from the graph, the measured distance between country pairs is very similar in both datasets. The mean difference between the Dynamic Gravity and CEPII distances is 4.4 kilometers while the median difference is 7.1 kilometers.
Figure 14 presents a set of comparisons between the Dynamic Gravity dataset, the CEPII dataset, and the Rose’s dataset for three additional types of variables. In all cases, Rose’s dataset has the lowest coverage, as it covers the smallest set of countries.
The top-left panel shows the number of country pairs that have at least one preferential trade agreement between them. The Dynamic Gravity dataset features nearly 50% more country pairs in trade agreements than CEPII. Although it can be difficult to determine conclusively given the lack of detailed information about the construction of the CEPII variables, we expect that this difference is the result of both a more period-appropriate set of countries in existence within each year and a more extensive set of trade agreements upon which the Dynamic Gravity dataset is based.
The top right panel of figure 14 shows the number of country pairs that have non-missing, non-zero observations for the GDP. Here, CEPII provides more coverage in the early years. Part of this additional coverage is due to countries in the dataset that did not yet exist, part is due to the presence of GDP figures from unspecified sources. Despite listing the WDI as the source of their data, the CEPII dataset features observations for countries and years that are not present in the WDI database.19 Thus, although the Dynamic Gravity dataset features fewer GDP records, they are guaranteed to originate from a consistent source and correspond to countries that existed as independent nations at the time.
Finally, the bottom left panel of figure 14 shows the number of country pairs with colonial ties. By construction, this number is constant in the CEPII dataset. It is growing over time in the Dynamic Gravity, reflecting the gradual growth on the number of countries becoming independent from their colonial hegemons in the early decades covered by the dataset. Among other potential benefits, this time variation supports improved econometric identification of colonial influences.
Because the primary use for this type of data is gravity analysis of international trade, we compare the Dynamic Gravity dataset to the Rose and CEPII datasets in a series of standard gravity model specifications. These comparisons provide validation that the Dynamic Gravity dataset is producing model results that are consistent with the trade literature. They also highlight some relative strengths of the Dynamic Gravity dataset from a practical perspective.
In each comparison, the Dynamic Gravity, CEPII, and Rose datasets are used to estimate standard gravity model specifications. Each of the three gravity datasets is combined with the same dataset of bilateral trade flows. The trade data originated from the UN Comtrade database and reflects all available total merchandise imports reported between the years 1989 and 2015.20 The data was expanded to include zero trade flows by “squaring” the data based on the set of countries present in the dataset within each year. That is, every possible pairing of countries is present each year, and if no trade is reported by Comtrade for a given pair, we assume the value is zero.21 This results in an initial trade dataset consisting of about 1.44 million records.
In each comparison described below, the following non-linear regression is estimated.
| (1) |
Here, denotes trade values between exporter and importer in year . Function denotes a linear combination of the exporter-year, importer-year, and importer-exporter gravity variables described in each specification below. In most specifications, measures for bilateral distance, shared borders, PTA membership, common language, colonial ties, and GDP were included. Finally, , , and denote exporter, importer, and year fixed effects, respectively, to control for multilateral resistances. While the inclusion of more granular fixed effects, such as importer-exporter or country-year, is common practice in the modern gravity literature, our desire to include country-specific variables such as GDP as a part of the comparisons informed this selection. All specifications were estimated using a Poisson Pseudo Maximum Likelihood procedure, as described in Santos Silva and Tenreyro (2005). This specification and estimation methodology follows standard practices in the gravity literature for structural gravity modeling. For example, the methodological survey papers by Head and Mayer (2014) and Piermartini and Yotov (2016) as well as the gravity meta-analyses of Disdier and Head (2008) and Cipollina and Salvatici (2010) describe similarly specified models.
The first of these comparison specifications aims to evaluate the three gravity datasets using a standard specification that utilizes variables present in all three sets. Specifically, we include variables reflecting GDP, geographic distance, shared borders, trade agreements, common languages, and colonial ties.22
The original trade data was mapped to each gravity dataset to the best extent possible. A selection of 174 countries was made based on those that were present in all three gravity datasets within the sample period, 1989–2015. In each case, there is a difference in the number of observations available upon which to regress. The Rose dataset results in the smallest number by a large margin, 73,022. Part of this is due to the limited coverage of years, another is due to the more limited number of countries present in early years. The Dynamic Gravity and CEPII datasets both exhibit substantially more observations: 713,064 and 735,841, respectively.
The difference between the total number of observations available using the Dynamic Gravity and CEPII datasets is the result of some nuanced differences in their ability to match with the trade data. Of the original trade data observations (prior to the reduction in the number of countries), only 11 percent fail to match with a corresponding record in the Dynamic Gravity set. By comparison, about 17 percent of the trade records fail to match with a record in the CEPII dataset. This implies that the Dynamic Gravity dataset features greater coverage of the country pairs present in Comtrade during the sample period.23 However, once merged, not all observations can be used for estimation; many exhibit missing values for at least one variable. The Dynamic Gravity data features an additional 15 percent of the records with a missing value in the gravity data. For the CEPII dataset, about 12 percent are lost due to missing values. In both cases, missing values for GDP are the root cause. As described in section 3, CEPII has supplemented their GDP figures with additional, unspecified sources, resulting in fewer missing observations than the Dynamic Gravity dataset.24
A second cause for the difference in the number of usable observations between the two datasets are the years in which certain countries are present in the data. Recall that the set of countries present in Dynamic Gravity dataset is variable over time based on independence and dissolution dates, reflecting the status of the world in each year. The CEPII dataset features a static set of countries present in every year. A consequence of this is that the mapping to trade data can be problematic with regards to countries that become independent, split, merge, or dissolve. Comtrade occasionally reports trade flows involving countries that are not independent. The CEPII dataset can match to some of these countries while the Dynamic Gravity dataset is unable to. As a result, there may exist trade flows in certain years that map to the CEPII dataset but do not map to the Dynamic Gravity set because the trading partner is not recognized as being independent in those years. An example of this is Hong Kong, which appears as a trading partner in Comtrade’s data prior to it first appearing in the Dynamic Gravity dataset in 1997.25
Table 1 presents the estimation results for equation (1) of this first comparison between the Dynamic Gravity dataset, the CEPII dataset, and the Rose dataset. The specifications differ slightly based on the fact that the Rose data does not report two of the variables as granularly as the other two datasets. Specifically, the GDP and colonial data series are each combined into single measures rather than importer- and exporter- specific measures.
| Dynamic Gravity | CEPII | Rose | |
| log(nominal GDP) of exporter | 0.6500 | 0.6267 | |
| (0.026) | (0.027) | ||
| log(nominal GDP) of importer | 0.6301 | 0.6463 | |
| (0.027) | (0.026) | ||
| log(Product of real GDPs) | -0.0871 | ||
| (0.039) | |||
| log(Distance) | -0.7507 | -0.7207 | -0.8582 |
| (0.011) | (0.011) | (0.026) | |
| Contiguity | 0.3430 | 0.4023 | 0.3017 |
| (0.019) | (0.019) | (0.064) | |
| PTA | 0.3327 | 0.3905 | 0.1588 |
| (0.018) | (0.020) | (0.014) | |
| Common language | 0.2185 | 0.1118 | 0.3583 |
| (0.017) | (0.019) | (0.048) | |
| Exporter colony of importer | 0.5033 | -0.0199 | |
| (0.040) | (0.040) | ||
| Importer colony of exporter | 0.6775 | 0.2164 | |
| (0.034) | (0.038) | ||
| Pair ever in colonial relationship | 0.3930 | ||
| (0.061) | |||
| Fixed effects | Yes | Yes | Yes |
| Number of observations | 713,064 | 735,841 | 73,022 |
As seen from table 1, the Dynamic Gravity and CEPII gravity data produce comparable results both in sign and, in most cases, magnitude. Many of the estimates using Rose’s data are similar as well, although less so than the other two. In fact, for variables that can be directly compared across all three data sources, the Dynamic Gravity estimates are reliably between those produced by the other datasets. Furthermore, the Dynamic Gravity dataset is the only one to produces p-values below one percent for all estimates. We compare the estimates produced using Dynamic Gravity and CEPII gravity controls using a simple z-test for equality of coefficients.26 The results of this test are shown in table 2. Estimates of the effects of log(GDP) and log(Distance) on bilateral trade flows produced using the two datasets do not differ beyond the 5% level of significance. This is because both datasets use similar source data and definitions for the GDP and population-weighted distance measures. On the other hand, the Dynamic Gravity estimates differ from those using CEPII gravity data for contiguity, trade agreement participation, common language, and colonial status. These variables, by their nature, are more likely to differ between the two datasets because of potentially different source data and definitions. In these cases, we suggest that our dataset more accurately measures these factors based on the thoroughness and precision of our research.
| z-score | |
| log(GDP) of exporter | 0.62 |
| log(GDP) of importer | -0.43 |
| log(Distance) | -1.93 |
| Contiguity | -2.21 |
| PTA | -2.15 |
| Common language | 4.19 |
| Exporter colony of importer | 9.25 |
| Importer colony of exporter | 9.04 |
*** , ** , * . | |
The second set of comparison specifications aims to test the three gravity datasets in a way that more closely matches all three datasets using a consistent set of years, countries, and variables available in all three datasets. Rose (2004) is the most restrictive of the three datasets, providing only one measure of GDP, a single non-directional colonial relationship per country pair, and data through 1999 only. We modify the Dynamic Gravity and the CEPII data to match the information available in the Rose specification by combining the GDP and colonial variables and limiting the estimation years to 1989–1999. As in the previous case, we perform the estimation for a selection of 174 countries present in all three datasets.
Table 3 presents the results of this comparison. As before, the Dynamic Gravity and CEPII datasets produce results that are similar in sign and magnitude, though there are some notable differences between the two. In particular, estimates for the log of distance and for the binary measure of whether a pair has ever been in a colonial relationship differ between the two sets of data. Notably, using CEPII gravity data to measure the effects of colonial relationships on trade in this specification produces an estimate that is not statistically significant, which is consistent with the estimates for “Exporter colony of importer” from comparison I.
| Dynamic Gravity | CEPII | Rose | |
| log(Product of real GDPs) | 0.3423 | 0.3641 | -0.0871 |
| (0.057) | (0.061) | (0.039) | |
| log(Distance) | -0.6766 | -0.6114 | -0.8582 |
| (0.018) | (0.019) | (0.026) | |
| Contiguity | 0.4469 | 0.5086 | 0.3017 |
| (0.037) | (0.042) | (0.064) | |
| PTA | 0.5339 | 0.6163 | 0.1588 |
| (0.034) | (0.046) | (0.014) | |
| Common language | 0.2507 | 0.2788 | 0.3583 |
| (0.030) | (0.032) | (0.048) | |
| Pair ever in colonial relationship | 0.7764 | 0.0141 | 0.3930 |
| (0.047) | (0.050) | (0.061) | |
| Fixed effects | Yes | Yes | Yes |
| Number of observations | 256,380 | 273,098 | 73,022 |
Table 4 shows how coefficients of the specifications using CEPII and Rose gravity data compare to those of the specification using Dynamic Gravity data. Comparing the Dynamic Gravity estimates to the CEPII estimates produces results similar to those described in section 4.1. Estimates from the specification using Rose’s dataset are all different from those produced using the Dynamic Gravity dataset.
| Dynamic Gravity
| ||
| vs CEPII, z-score | vs Rose, z-score | |
| log(Product of real GDPs) | -0.26 | 6.22 |
| log(Distance) | -2.49 | 4.23 |
| Contiguity | -1.10 | 1.97 |
| PTA | -1.44 | 10.20 |
| Common language | -0.64 | -1.90 |
| Pair ever in colonial relationship | 11.11 | 4.98 |
*** , ** , * . | ||
This paper introduces the newly constructed Dynamic Gravity dataset, presents selected summary information, and compares this dataset to two popular sources of gravity variables.
The Dynamic Gravity dataset provides several advancements over previously available data. We introduce a rich set of countries that enter the sample as they gain independence from other nations and exit the sample upon dissolution. To track changes in existing countries, we introduce a new dynamic country code that identifies these changes. We add variables that were not previously available in gravity datasets such as measures of political stability and production capacity. We introduce time and magnitude variation to previously existing variables, such as measures of conflict. Finally, we take great care to describe the construction of the dataset in extensive documentation.
We highlight some similarities and differences between the Dynamic Gravity dataset and two other commonly used gravity datasets: the CEPII dataset and Andrew Rose’s dataset. We then validate the integrity of the Dynamic Gravity dataset by comparing its performance in a standard gravity model against these two datasets. The results of these regressions indicate that the Dynamic Gravity dataset produces estimates that are consistent with these alternative datasets and the literature. In several cases—GDP and distance measures—the estimates do not differ statistically from those produced by the CEPII dataset. In other cases—contiguity, PTAs, common languages, and colonial relationships—the Dynamic dataset produces qualitatively similar but quantitatively different estimates. These findings suggest that the Dynamic Gravity dataset is an indistinguishable substitute for many of the variables most often used in gravity modeling. In cases where they differ, we believe that this is an improvement over existing datasets due to the transparency and thoroughness of our construction.
The World Factbook 2017. Central Intelligence Agency, Washington, DC, 2017.
J. Anderson and Y. Yotov. The Changing Incidence of Geography. American Economic Review, 100:2157–2186, 2010.
Maria Cipollina and Luca Salvatici. Reciprocal trade agreements in gravity models: A meta-analysis. Review of International Economics, 18(1):63–80, 2010. doi: 10.1111/j. 1467-9396.2009.00877.x.
Correlates of War Project. Colonial Contiguity Data, 1816–2016. Version 3.1. 2017.
Anne-Célia Disdier and Keith Head. The Puzzling Persistence of the Distance Effect on Bilateral Trade. The Review of Economics and Statistics, 90(1):37–48, 2008. URL https://www.jstor.org/stable/40043123.
Robert C. Feenstra, Robert Inklaar, and Marcel P. Timmer. The Next Generation of the Penn World Table. American Economic Review, 105(10):3150–3182, 2015. available for download at www.ggdc.net/pwt.
Tamara Gurevich, Peter Herman, Serge Shikher, and Ricky Ubee. Extending the CEPII Gravity Data Set. 2017. URL https://www.usitc.gov/publications/332/cepii-update-v3.pdf.
Tamara Gurevich, Peter Herman, Nabil Abbyad, Meryem Demirkaya, Austin Drenski, Jeffrey Horowitz, and Grace Kenneally. The Dynamic Gravity Dataset: Technical Documentation, 2018. Version v1.00.
K. Head and T. Mayer. Gravity Equations: Toolkit, Cookbook, Workhorse. In Gopinath, Helpman, and Rogoff, editors, Handbook of International Economics, volume 4. Elsiver, 2014.
K. Head, T. Mayer, and J. Ries. The erosion of colonial trade linkages after independence. Journal of International Economics, 81(1):1–14, 2010.
Monty G. Marshall, Ted Robert Gurr, and Keith Jaggers. Polity IV Project Dataset User’s Manual, v.2016. Polity IV Project, 2016.
T. Clifton Morgan, Navin Bapat, and Yoshiharu Kobayashi. Threat and imposition of economic sanctions 1945–2005: Updating the TIES dataset. Conflict Management and Peace Science, 31(5):541–558, 2014. doi: 10.1177/0738894213520379.
Alessandro Nicita and Marcelo Olarreaga. Trade, Production, and Protection Database, 1976–2004. World Bank Economic Review, 21(1):165–171, 2007.
Roberta Piermartini and Yoto V Yotov. Estimating Trade Policy Effects with Structural Gravity. 2016.
Andrew K. Rose. Do We Really Know That the WTO Increases Trade? American Economic Review, 94(1):98–114, 2004.
Joao Santos Silva and Silvana Tenreyro. The log of gravity. The Review of Economics and Statistics, 88(4):641–658, 2005.
The World Bank, 2016. URL https://data.worldbank.org/data-catalog/world-development-indicators.
The World Trade Organization (WTO). Regional Trade Agreements Information System (RTA-IS); User Guide, 2017a. URL https://rtais.wto.org/UserGuide/RTAIS{\_}USER{\_}GUIDE{\_}EN.html{\#}{\_}Toc201649641.
The World Trade Organization (WTO). Regional Trade Agreements Information System (RTA-IS), 2017b. URL rtais.wto.org.
1See Head and Mayer (2014) for a comprehensive review of estimation and interpretation of gravity equations in trade models.
2Other popular sources of gravity variables include the Rose (2004) dataset, the Anderson and Yotov (2010) dataset, and various Trade and Production datasets stemming from the work of Nicita and Olarreaga (2007) and the World Bank. While none of these datasets were created specifically to be used as stand alone gravity datasets, they have gained some prominence among researchers. All of these datasets are discussed in detail in Appendix B.2 of Head and Mayer (2014).
3The CEPII gravity dataset can be downloaded from https://www.cepii.fr/cepii/en/bdd_modele/presentation.asp?id=8.
4For example, the CEPII dataset recognizes only one conflict for the United States, which is with Great Britain, and likely dating back to the war of 1812.
5While the Dynamic Gravity dataset is suited for use outside of international trade research, the list of recognized countries is heavily based on the international trade statistics with which we foresee it being used.
6The names of variables are distinguished using the convention “_o” for origin and “_d” for destination.
7ISO codes are maintained by the International Organization for Standardization (IOS). For more information on ISO3 codes see https://www.iso.org/home.html
8The countries were Guadeloupe, Kiribati, Malaysia, Netherlands Antilles, Pakistan, Panama, Saudi Arabia, Serbia, South Africa, Sudan, Vietnam, and West Germany.
9The Penn World Tables can be downloaded from the Groningen Growth and Development Centre at https://www.rug.nl/ggdc/productivity/pwt/; the World Bank data are available at https://data.worldbank.org/.
10The large drop in the number of country pairs in an FTA or goods-only trade agreement in 1992 is primarily the result of the dissolution of the Third Convention of Lomé in September of 1991. The agreement was a relatively large FTA among more than 50 countries in Africa, the Caribbean, Europe, and the Pacific.
11For complete documentation on the Regional Trade Agreements Information System see WTO, 2017a.
12https://www.cia.gov/library/publications/the-world-factbook/
13https://www.correlatesofwar.org/data-sets/
14https://www.systemicpeace.org/polity/polity4.htm
15For example, records are missing for Afghanistan between 2001 and 2013 and countries that have recently been involved in conflicts, such as East and West Germany in the years following World War II.
16https://www.correlatesofwar.org/data-sets/MIDs
17For more information and to download the data see https://www.unc.edu/~bapat/TIES.htm
18Further comparisons with the Rose dataset are left for the gravity estimations in section 4.
19For example, the CEPII dataset reports GDP figures for Russia more than 20 years before the dissolution of the Soviet Union. We have not been able to determine a source for observations like these.
20Trade data was downloaded from https://wits.worldbank.org/. Selected years reflect a period of thorough coverage with respect to the trade data and were not chosen based on any requirements of the gravity datasets with which it is being combined.
21See Piermartini and Yotov (2016) for a discussion of zero trade flows in gravity modeling.
22The Dynamic Gravity dataset version includes the variables gdp_wdi_cur_d, gdp_wdi_cur_d, distance, contiguity, agree_pta, common_language, colony_of_destination_ever, and colony_of_origin_ever. The CEPII dataset version includes gdp_o, gdp_d, distw, contig, fta_wto, comlang_off , col_to, and col_fr. The Rose dataset version includes lrgdp (the product of GDPs), ldist, border, rta, comlang, colony (non-directional colonial relationship).
23The trade flows that do not match are primarily those corresponding to non-standard trading partners or aggregates such as “World” (WLD), “Belgium-Luxembourg” (BLX), or “Bunkers” (BUN).
24From a practical perspective, the inclusion of more GDP figures is likely of limited value. Most modern gravity research includes country or country-year fixed effects that fully control for GDP effects, rendering the inclusion of that data unnecessary. See Piermartini and Yotov (2016) for a deeper discussion of fixed effect strategies.
25Countries report imports from Hong Kong in all years within our sample period. Meanwhile, Hong Kong appears to first report imports in 1993.
26We forgo making this comparison to the Rose data results until the next section because of the differences in how several of the variables are defined.