ECONOMICS WORKING PAPER SERIES
IDENTIFYING MULTILATERAL DEPENDENCIES
IN THE WORLD TRADE NETWORK
Peter R. Herman
Working Paper 2017–04–A
U.S. INTERNATIONAL TRADE COMMISSION
500 E Street SW
Washington, DC 20436
April 2017
Office of Economics working papers are the result of ongoing professional research of USITC Staff and are solely meant to represent the opinions and professional research of individual authors. These papers are not meant to represent in any way the views of the U.S. International Trade Commission or any of its individual Commissioners. Working papers are circulated to promote the active exchange of ideas between USITC Staff and recognized experts outside the USITC and to promote professional development of Office Staff by encouraging outside professional critique of staff research.
Identifying Multilateral Dependencies in the World Trade Network
Peter R. Herman
Office of Economics Working Paper 2017–04–A
Abstract
When studying the formation of trade between two countries, traditional modeling has described this decision as being primarily dependent on characteristics of the two trading partners. It is likely the case, however, that this decision to trade is dependent not only on the two countries involved but on the patterns by which all partners trade with one another. Standard efforts to control for these higher level dependencies such as the inclusion of multilateral resistance measures provide only a blunt reflection of these dependencies and neglect valuable information that the global trade network contains. This paper proposes the explicit incorporation of higher level dependencies in traditional modeling frameworks. Two network-based, gravity-inspired approaches are considered–a probit model of trade incidence and an exponential random graph model. Each approach uses the structure of the entire world trade network to explain the formation of trade between individual of countries. The use of exponential random graph modeling techniques (ERGM) in particular, which have largely been unexplored in economics, provides a powerful yet flexible framework with which to model and estimate bilateral trade in a way that allows for the identification of a wider variety of multilateral dependencies and a deeper consideration of the patterns that emerge in the world trade network. Using a standard gravity data set, a series of probit and ERGM estimations are conducted for observed world trade networks. The results from these models provide strong evidence that higher level dependencies are present in international trade and that ERGM analysis represents an effective modeling environment in which to study them.
JEL Classification: F14, D85
Peter R. Herman
Research Division
Office of Economics
U.S. International Trade Commission
peter.herman@usitc.gov
Understanding the determinants of trade has long been a significant interest in the field of international trade. Conventional work has focused on the ways in which trade between two countries is affected by the characteristics of those two countries as well as the relationships between them. However, this research typically omits potential dependencies between these two countries’ trade and other countries with whom they have relationships. It is likely the case that trade flows between any two countries are affected not only by the relationships between those two countries (primary dependencies) but by the relationships present between those two countries and other external countries (secondary dependencies), or the relationships between any other combination of external trading partners (tertiary dependencies). By ignoring these higher level dependencies, significant determinants of trade are overlooked.
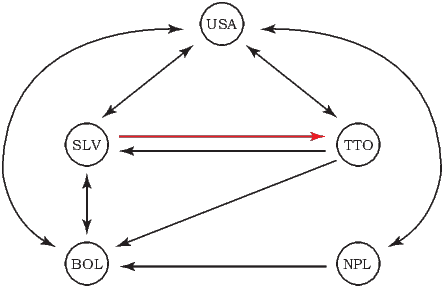
To illustrate these potential dependencies, figure 1 depicts the trade flows between the United States, El Salvador, Trinidad and Tobago, Bolivia, and Nepal in 1999. When considering the trade occurring between two countries such as exports from El Salvador to Trinidad and Tobago, it is likely the case that the other links in the network affect this trade flow. For example, the fact that both countries trade with the United States or that Bolivia does not export to Trinidad and Tobago may influence their decision to trade. In both cases, these effects would represent secondary dependencies. Additionally, it may be the case that the trade between the U.S. and Bolivia or Nepal impacts the decision of El Salvador to export to Trinidad and Tobago as well, which would represent a tertiary dependency. While traditional international trade has a long history of effectively identifying the primary dependencies within trade, it has has made limited progress with respect to these higher level dependencies.

The purpose of this paper is to propose the use of network based approaches to describe international trade relationships in a way that explicitly incorporates higher level dependencies. International trade can be described in terms of a network in which trading partners are represented by nodes in the graph and relationships between those countries can be expressed by links between their respective nodes. For example, figures 2, 3, and 4 depict three network structures commonly studied within international trade. In each of the three graphs, nodes represent countries organized by geographic location while the links represent different information in each case. The first, figure 2, depicts trade flows between countries such that a link from a country to a country exists if exports to . Additionally, the network is weighted by the value of those trade flows such that the link is darker and thicker for larger values of trade. The second graph, figure 3, depicts common language relationships such that a link exists if at least 9% of the population in both countries speaks a common language. The final graph, figure 4, depicts the network of shared common borders. The notion of higher level dependencies can be explained by recognizing that the decisions of a country to trade with any other country is likely dependent on its position in each of these networks as well as others. In addition to the relative characteristics of and , this decision will be impacted by the other links and nodes to which it is connected as well as those that it does not connect to directly. In order to fully understand the decision to trade with a given partner, it is critical that these higher level effects be introduced to models of international trade.
In order to identify these types of higher level multilateral dependencies, two modeling approaches are considered. The first approach follows a conventional line of literature using a probit model of trade incidence. The model is essentially an extension of the first stage of a two-stage gravity model, as described in Helpman et al. (2008). It differs, however, due to the inclusion of a collection of network characteristics such as reciprocal and triangular trading relationships that capture higher level dependencies. The second method approaches the analysis as a network formation problem, using an empirical network analysis tool known as exponential random graph modeling (ERGM).
The ERGM framework represents an especially appealing approach for studying higher level dependencies in trade. The methodology identifies higher level dependencies by modeling the formation of the network and each of its links as being conditional on the full structure of the network as well as other relevant networks. The observed international trade network is considered one of a multitude of possible networks that could have formed so that the actual trade network represents a realization of a random variable drawn from a distribution of all the possible world trade networks that could have arisen given the set of trading partners. Within this framework, statistical inference that aids in the understanding of the underlying distribution of possible networks is possible and helps explain why the observed trade network formed instead of any of the other possible networks.
The random graph model is specified by defining a set of network attributes and respective weights upon which link formation is dependent. These attributes are commonly topological features of the network such as reciprocal links in which imports from to and from to are both present in the network or triangles in which three countries are linked with one another in at least one of several possible patterns. Alternatively, these attributes may contain social selection features such as homophily in which similarities between countries such as shared common languages affect trade formation. Using a combination of topological and social selection attributes, key features of customary bilateral trade research such as common languages, GDP products, and colonial ties can be considered while also accounting for potentially important higher level dependencies like trade reciprocity.
Estimations of several random graph models described in the following sections provide strong evidence that higher level dependencies significantly affect international trade. A series of three models are proposed based on three assumed dependency structures composed of topological and social selection attributes. The models are composed of numerous bilateral trade determinants present in traditional trade research as well as several higher level network dependencies that are typically absent in other studies. These models are estimated with a Markov Chain Monte Carlo procedure using several international trade networks derived from bilateral trade data. The results generally indicate that the ERGM estimations are consistent with previous research but also identify statistically significant higher level dependencies in the formation of trade relationships that are typically overlooked.
Most research on bilateral trade determinants has been based on the estimation of gravity trade models. In recent years, authors have identified the importance of network relationships within this framework and have attempted to incorporate aspects of networks into these models. Much of this research has worked to properly identify and include a variety of potentially significant network relationships such as distance, common borders, common languages, and cultural ties. In particular, Rauch (1999) provides strong evidence that these network relationships have a significant impact on trade. Following this work, many papers have built on these findings by providing deeper analysis and alternative measurements for each of these network relationships. For example, Brun et al. (2005) and Berthelon and Freund (2008) examine the role of georgraphic distance between countries in the trade network. Work such as Hutchinson (2005), Ku and Zussman (2010), and Melitz (2008) study the ways in which countries relate through common language networks. In a similar vein, Rauch and Trindade (2002), Linders et al. (2005), Hofstede (1980), and Felbermayr and Toubal (2010) analyze the effect of cultural networks on trade.
Beyond these conventional notions of network relationships, most recent literature has attempted to control for some implicit aspects of network relationships through the incorporation of multilateral resistance terms. Originally introduced by Anderson and van Wincoop (2003), multilateral resistance terms are intended to identify unobserved barriers to trade between two trading partners. Anderson and van Wincoop incorporate these terms in the form relative price effects estimated using a series of implicit functions composed of the prices in all countries. By attempting to include information about global prices, some aspects of the entire network are included through multilateral resistance terms and provide confirmation that the network at large is important but this methodology fails to fully utilize the information available or recognize other important ways in which the network influences trade beyond relative prices.
In each of these papers, as well as many more, the notions of network dependency are present but are typically severely limited in their dimension. Each describes one aspect of network relationships such as a secondary network when evaluating the effects of common language or higher level node effects through multilateral resistances but these papers do not truly explore the role of higher level dependencies in trade. Recently, however, more research has been appearing that attempts to explain the role of these higher level dependencies within the world trade network.
A number of recent papers have studied the world trade network from a topological perspective that explicitly identifies network properties. Work by De Benedictis and Tajoli (2011), De Benedictis et al. (2013), and Deguchi et al. (2014) identify typical graph features of the world trade network such as density, clustering, and centrality measures. De Benedictis and Tajoli (2011) compare centralization measures that reflect how well connected nodes are across a variety of countries or regions and identify the countries that operate as trade “hubs”. For example, the authors show that the WTO was effective in increasing the density of the trade network (i.e. the number of links). De Benedictis et al. (2013) provide a similar but deeper analysis of several centrality measures. They find that degree centrality, which reflects how well connected a given node is, may be a strong indicator of trade surpluses or deficits. Closeness centrality or geodesic distance, which reflect the minimum number of links separating two nodes, indicate how well connected a node is to the rest of the world. Finally, eigenvalue centrality, which reflects how well connected a node’s partners are, offers insight into the role of secondary dependencies among trading partners. Deguchi et al. (2014) follow this line of research on centrality by creating a ranking similar to the Page-Rank algorithm.1 Using this ranking, they observe changes in the positions of countries within the list and find, for example, that China has grown to become the highest value hub while Japan and others have dropped over time. These papers offer an important new perspective on trade by studying the properties of the network as a whole and identifying important aspects of trade that are missed by traditional gravity trade models.
Few papers, however, go beyond making observations about the world trade network as it exists. A key question, and one that is central in understanding bilateral trade determinants, is why the current world trade network arose rather than any of the other possible network configurations. Understanding the formation of the network is critical in understanding the greater question of why trade occurs between pairs of countries. Few papers address this question directly but it is a growing area of interest.
One such example is the recent work by Chaney (2014). Chaney utilizes a network model to describe growth at the extensive margin. The author specifically looks at the tendency with which exporting firms use concurrent trading partners to match with new, more distant partners. If matching difficulty is increasing in the distance between firms, current partners may be used to reduce that barrier and shorten the effective distance to the new firm. Using firm-level French data, Chaney finds evidence such as accelerating growth in the distance of trade for the observed firms that supports this proposition. Within the context of the present paper, these results provide confirmation that higher level network relationships are influential. The concept of using one partner to assist in the linking with another partner can be reflected through the presence of a specific type of triangular relationship known as a transitive triple. Thus, Chaney’s results can be interpreted as providing support for the modeling of bilateral trade with higher level dependencies.
Similarly, Dueñas and Fagiolo (2013) study properties of the world trade network through a gravity framework. The author’s estimate standard gravity models and use the estimated parameters to predict link formation and generate simulated trade networks. These trade networks are compared to observed trade networks in order to determine if gravity models are capable of explaining customary topological features of trade networks. They find that gravity models are often effective at replicating some aspects of trade networks, predominantly first order characteristics such as average node degree, but perform poorly at predicting higher order characteristics such as clustering unless the presence of links is fixed and only the weights are predicted. Much of their difficulty in generating similar networks stems from an general inability to accurately replicate binary link formation, which is a primary focus of the work in the present paper.
In terms of providing a comprehensive study of higher level effects in international trade, the best example is Ward et al. (2013). Similar to the present paper, the authors assert that dependencies exist between links and nodes within the network and attempt to empirically study these higher level dependencies in international trade. However, rather than the ERGM methodology proposed here, they study this problem using an alternative general bi-linear mixed effects model (GBME) based on the work of Hoff (2005). A GBME model studies the structure of a network through a process similar to ANOVA. Links between nodes are estimated such that the error terms are modeled as being composed of dyad-level random effects. Using these decompositions of variance, many aspects of network dependencies can be identified including reciprocity, sender and receiver effects, and third-order effects similar to triangles. Ward et al. find that higher level network effects improve the explanatory power of the gravity model and result in significantly higher values when the considered network effects are included.
GBME models were proposed as an alternative to early ERGM specifications in order to estimate valued networks, which represents a current limitation for ERGMs. While this is a significant strength in studying bilateral trade flows, GBME models face some relative weaknesses as well. Because GBME models identify higher order dependencies by decomposing error terms into specific functional forms, they necessarily impose a considerable amount of structure on the estimation problem, thereby limiting the types of dependencies that can be incorporated. By comparison, ERGMs exhibit a large amount of flexibility in modeling the dependence structure of the network due to the additive nature of the attributes included in the exponential random graph function. Thus, while there may be considerable overlaps in the objectives of the present paper and Ward et al. (2013), the work presented here intends to not only provide additional affirmation of the importance of higher-order network effects in international trade but also show that ERGMs represent an effective means of studying them.
The paper proceeds as follows. Section 2 presents the probit approach to modeling higher level dependencies in trade. Section 3 describes the ERGM modeling framework and estimation procedures. Section 4 presents the ERGM estimations of international trade. Section 5 concludes.
Before examining the proposed ERGM methodology in depth, it is worth analyzing higher level dependencies in trade within a more customary gravity framework. Doing so provides strong evidence that these types of dependencies are prevalent and that a modeling approach that is specially tailored to the consideration of network dependencies, such as ERGM analysis, is worth pursuing.
The analysis of trade formation has been a mainstay in international trade research given its relevancy in analyzing the extensive margins of trade as well as coping with zero-trade issues. Helpman et al. (2008) provide one such methodology using a two-stage gravity estimation which is considered here given its close relation to the modeling objectives of ERGMs. The authors propose a two-step method for estimating gravity in which the first stage estimates the selection of trading partners into trading while the second stage estimates trade flows conditional on that selection. Of specific interest here is the first stage which models the formation of trade between partners. In this stage, the probability of trade formation, which is analogous to link formation in the trade network, is estimated using a probit model composed of traditional trade influences such as distance, common borders, and language ties.
Similar estimations are undertaken in order to identify the extent to which network attributes influence trade formation and improve model performance using a traditional methodology. In what follows, let and denote an importing and exporting country, respectively, and denote the absence or presence of trade between them, respectively. In line with standard gravity approaches, is modeled as being a function of their GDPs, distance apart, contiguity, language or colonial ties, regional trade agreements, and a collection of fixed effects. Additionally, three types of network attributes are added to the model in order to identify potential network dependencies. The first of these attributes is an indicator for mutual trade. This mutual dummy takes the value of one for trade between and if imports from during that same year. The second class of network attributes, consisting of two variables, reflects the presence of three-way trade. The first of these variables counts the number of transitive trading relations shared by and . A transitive relationship occurs if there exists a country such that imports from , imports from , and imports from . The constructed variable counts the number of countries for which the existence of trade from to would complete a transitive triple. Similarly, the second three-way variable counts the number of cyclical relationships which consist of countries such that imports from and imports from . Finally, the third class of network attributes consists of degree measures that reflect network density and the number of trade relationships maintained by and . Four specific measures are considered for each period: the importer-import degree which counts the number of countries imports to, the importer-export degree which counts the number of countries exports to, the exporter-export degree which counts the number of countries exports to, and the exporter-import degree which counts the number of countries imports to. Table 1 summarizes these attributes.
| Class | Attribute | Specification |
| Mutual Trade | Reciprocal Tie | |
| Three-Way Trade | Transitive Triple | |
| Cyclical Triple | ||
| Degrees | Importer-import | |
| Importer-export | ||
| Exporter-export | ||
| Exporter-import | ||
I estimate three specific probit models given by equations (1), (2), and (3).
| (1) |
| (2) |
| (3) |
denotes the set of gravity variables specified above, denotes the set of network attributes, and , , and denote importer, exporter, and year fixed effects respectively. The data used in the estimation comes from the from the BACI bilateral trade and gravity data sets provided by CEPII (see Gaulier and Zignago (2010) and Head et al. (2010), respectively). Model (1) is provided as a baseline model. Model (2) introduces the network attributes. It is likely that there is some overlap between the considered network attributes and traditional multilateral resistances being controlled for using fixed effects. To provide insight on this possible overlap, model (3) drops these fixed effects so that estimates and model fit can be compared.
| (1) | (2) | (3) | |
| 0.0670 (0.0193) | -0.0157 (0.0186) | 0.104(0.005) | |
| 0.202 (0.020) | 0.0475 (0.0192) | 0.0880(0.005) | |
| Distance | -0.685 (0.012) | -0.596 (0.012) | -0.452 (0.011) |
| Contiguous | -0.207 (0.095) | -0.131 (0.089) | -0.0478 (0.085) |
| Language/Colony | 0.325 (0.021) | 0.294 (0.021) | 0.270 (0.018) |
| RTA | 0.774 (0.050) | 0.664 (0.048) | 0.828 (0.048) |
| Mutual | 0.628 (0.012) | 0.764 (0.012) | |
| Transitive Count | 0.00876 (0.0009) | -0.00448(0.0006) | |
| Cyclical Count | 0.00477 (0.00080) | -0.00092 (0.00063) | |
| Importer-import Degree | 0.0187 (0.0005) | 0.0236 (0.0004) | |
| Importer-export Degree | -0.00251 (0.00055) | -0.00388 (0.0004) | |
| Exporter-export Degree | 0.0127 (0.0006) | 0.0262 (0.0004) | |
| Exporter-import Degree | -0.00171 (0.00049) | -0.00690 (0.0004) | |
| Constant | 3.469 (0.296) | 0.431 (0.291) | -1.782 (0.100) |
| Importer, Exporter, & Year F.E.s | yes | yes | no |
| 362074 | 362074 | 362074 | |
| pseudo | 0.556 | 0.595 | 0.570 |
| AIC | 214191.0 | 195422.9 | 206718.1 |
| ll | -106717.5 | -97326.4 | -103345.0 |
Table 2 provides a summary of the model estimates. In both models that include network attributes, these attributes are generally significant suggesting that higher level dependencies exist and influence trade formation. Mutual trade is positively correlated and similar in magnitude to RTAs, supporting the simple story that partners trade with one another in a mutual fashion. Three-way trade suggests a more complicated relationship as its sign is dependent on the inclusion of fixed effects. A possible interpretation is that these attributes are picking up features of both general trade expansion and unobserved restrictiveness. In the first case (model (2)), fixed effects are picking up unobserved aspects of country-specific trade restrictiveness (see, for example, Fontagné et al. (2016)). With these unobserved measures accounted for in the fixed effects, the magnitude of the two three-way trade variables are largely influenced by the general expansion of trade between all parties. If countries are trading with one another more frequently, the likelihood of any particular pair trading increases as well, as indicated by the positive coefficient. In comparison, by excluding fixed effects in model (3), aspects of trade restrictiveness may be reflected in the presence or absence of three-way trade. In this case, the presence of trade with a third country may reflect trade diversion as a result of unobserved restrictiveness and suggest a lower likelihood of trade. The coefficients for the degree attributes suggest further interesting relationships. The importer-import degree and exporter-export degree both imply that countries that import (export) with many partners are more likely to import (export) from one additional partner. On the other hand, the importer-export degree and exporter-import degree suggest that high importing (exporting) countries are less likely to export (import) themselves. Taken together, these results suggest the countries tend to specialize as either widely importing or exporting countries.
The next notion to address is the difference between models (2) and (3). As discussed before, the purpose of model (3) is to identify relationships between the network attributes and traditional multilateral resistances. Model (3) includes the network measures but omits the fixed effects commonly used to control for multilateral resistances. What we observe is that the inclusion of only the network measures results in model fit indicators that outperform those of model (1), which includes multilateral resistances but not network measures. The psuedo R and loglikelihood measures are both higher while the Akaiki Information Criterion is lower for model (3) than for model (1). This observation suggests that the relatively small collection of network characteristics considered here have more explanatory power than a conventional means by which trade models explain multilateral resistance.
What is most important about these observations is that these higher level dependencies are clearly present in international trade yet are largely unidentifiable within traditional methodologies. ERGM analysis, by comparison, provides a framework that is capable of explicitly modeling these dependencies.
When thinking about the emergence of networks in trade or any other environment, a common and compelling question is why did the observed network arise instead of any of the numerous other possible networks that could have been formed? By using the mathematics and statistics made available by representing modeling environments as networks, considerable insight can be gained in regards to this question. ERGM analysis is one such methodology that will be described in this section and tested in the section to follow.
A network consists of a collection of nodes and links that indicate relationships between these nodes. A significant motivation for the use of networks stems from the fact that this broad framework can be used to express a wide variety of economic environments in which the pattern by which agents relate to one another has a consequential bearing on behavior on agent activities. Within the context of international trade, networks can be used to describe complex trading relationships in which trading partners are represented by nodes in the networks and links can be used to describe a wide range of relationships such as trade flows, common languages, colonial ties, and shared borders. By studying the structure of these networks, considerable information can be gained about the patterns of trade.
A network can be represented mathematically with relative ease. Let denote the set of nodes in a network and denote a specific node within that set. Nodes are connected by links such that exists if there is an link extending from node to node . Networks can be unweighted, in which case such that indicates the presence of a link and indicates its absence, or they can be weighted, in which case specifies not only the existence of a link but its heterogeneous value. Furthermore, a network can be either directed, in which case arcs and are distinct, or undirected, in which case .
In the context of international trade, networks exhibiting a variety of these characteristics are common. For example, the extensive margin of trade could be sufficiently modeled using an unweighted network in which links represent the existence of trade between partners. However, a study of the intensive margin of trade would require the use of weighted networks in which links describe the actual volume of trade between both partners. In both cases, the network would generally need to be directed because exports from country to country are distinct from the exports from to . By comparison, a network depicting the presence of a shared common language between partners could be sufficiently described by an undirected network.
It is often convenient to represent the network using an adjacency matrix such that rows and columns represent origin and destination nodes, respectively. Thus, each cell in the matrix represents a link and the value of that cell reflects its value or weight.
It may also be the case that a set of nodes are related by more than one network. For example, countries are linked through a considerable number of possible networks such as trade flows, common languages, colonial ties, or regional trade agreements. In what follows, these different networks will be denoted using alternative variables to represent links in each network. For example, the set of links and may be used to denote trade flows and common language ties, respectively.
In addition to a range of different types of links that exist between nodes, nodes may also feature node-specific characteristics. For each node , there may exist a corresponding set of traits with typical elements . If the nodes represent countries, the set of node traits may include information such as GDP, GDP per capita, or WTO membership. One motivation for including node characteristics is that it allows for the study of social influences such as homophily. Homophily represents a tendency for nodes to link to other similar nodes. For example, countries belonging to preferential trade unions may be expected to trade more with other members than with non-members.
Given the unique ability of network structures to convey numerous dimensions of information, they yield themselves to a variety of powerful analytical options. ERGMs are one such way in which to study the structure of networks by identifying the specific aspects of a network that result in the likely formation of the networks that are ultimately observed. Beginning with the seminal work of Frank and Strauss (1986), ERGMs have become increasingly popular in the analysis of networks, predominantly in the areas of psychology, sociology, and statistics. More recent work such that by Wasserman and Pattison (1996) , Snijders (2002), Robins et al. (2007), and Lusher et al. (2013) has expanded on this framework and created a robust set of analytical tools with which to study networks.
The ERGM methodology views a network as a realization of a random variable. Networks are drawn from a distribution of possible networks such that the distribution is dependent on certain network attributes that will be described in greater detail shortly. Given these attributes and the implied distribution, some networks are more likely than others. Statistical inference on a particular observed network is possible by estimating the characteristics of the underlying distribution that lead to the realization of the observed network. Specifically, the distribution parameters that result in the observed network being the most likely network to have been formed are sought.
Following the definitions presented in Robins et al. (2007) and Lusher et al. (2013), an ERGM specifies the probability of a particular network realization in the following way.
| (4) |
The probability is given by an exponential function of parameters and network attributes . The network attributes are selected based on the assumed conditional dependencies in the model. For example, one such dependency might be mutual ties reflecting a reciprocal relationship. In this case, the attribute would be equal to the total number of mutual ties in the network. The parameters indicates the relative weight of each network attribute. In the example of mutual ties, a large positive parameter value would indicate that networks with many mutual ties are more likely and that the likelihood of an individual link forming is marginally higher if it completes a reciprocal relationship. Following the work of Frank and Strauss (1986), a homogeneity assumption is generally included with respect to the parameters and attributes. Homogeneity assumes that all linking patterns of the same type have the same effect. To illustrate what is meant by this, it assumes that the tendency for a mutual tie to form between two nodes and is identical to the tendency for a mutual tie to form between any other pair of nodes. Finally, the function is a normalizing coefficient that insures that the distribution is a proper probability distribution.
In specifying the model to be considered, assumptions about dyadic dependency must be made. These assumptions are incorporated by including network attributes that measure the assumed type of dependencies. Wasserman and Pattison (1996) and Lusher et al. (2013) provide extensive discussions and tables of typical network attributes used ERGM analysis. A subset of some of the most commonly used attributes is presented here in table 3 and table 4. In general, these network attributes can be arranged into two groups of attribute types: topological attributes and social selection attributes.
| Attribute | Description |
|
| Edges | Number of edges and, indirectly, the density of the network |
|
| Transitive Triples | Frequency that three nodes link such that links to , links to , and links to | |
| Cyclical Triples | Frequency that three nodes link such that links to , links to , and links to | |
| Triangles | Frequency that three nodes link in any pattern. | Transitive Cyclical Triples |
| Mutual Ties | Frequency that two node link reciprocally such that links to and links to |
|
| Out-2-Star | Frequency that one node links to two other nodes such that links to and |
|
| In-2-Star | Frequency that two nodes link to a common node such that and link to |
|
| Attribute | Description |
|
| Homophily | Effect of common node-attributes |
|
| Sender Effect | Effect of the node-attribute of the node of origin |
|
| Receiver Effect | Effect of the node-attribute of the destination node |
|
The topological attributes describe specific patterns of links within the network. Typical examples include a measure of density, -stars, triangles and triples, or mutual ties. Density reflects the number of links relative to the number of possible links and indicates whether the network is generally well connected or sparsely connected. A -star is a node that is connected to other nodes and may provide information as to the distribution of the number of links that nodes exhibit and notions of centrality.2 Triangles and triples describe patterns of relationships between three nodes.3 Mutual ties indicate pairs of nodes that both link to one another, indicating a reciprocal relationship. The use of these types of topological attributes allows for the inclusion of dyadic dependence in network models. Within the context of international trade, it allows for an explicit description of the ways in which the exports from one partner to another are affected by the other trade relationships of each partner and other countries.
The social selection attributes, by comparison, are based on aspects of the network in addition to the mere presence of links. It is through these attributes that secondary networks or node characteristics influence the formation of links. Common social selection attributes include measures of homophily, sender effects, and receiver effects. As described before, homophily refers to the possibility that nodes tend to link to similar nodes with a higher likelihood. Sender and receiver effects indicate whether certain unilateral characteristics affect the number of links extending from or to a node, respectively. In the context of international trade, social selection attributes can be included to model traditional trade determinants such as GDP, preferential trade agreements, or other country level effects.
An appropriately specified ERGM is one in which the set of attributes fully accounts for the assumed dependencies across nodes. One of the benefits of this modeling structure is there is a considerable amount of flexibility with regard to model construction. For example, Lusher et al. (2013) and Robins et al. (2007) describe two common dependency structures. The first is a Bernoulli random graph in which all links are assumed to be independent of one another. This assumption represents what is essentially the simplest possible structure where link formation is not dependent on any other links in the network. The model itself simply specifies the set of attributes as consisting of only a measurement of the number of links in the network. The second structure is a Markov graph and incorporates more significant dependency assumptions. A Markov random graph assumes that a link between two nodes is dependent on all links connecting to or from those nodes. The set of attributes for a Markov graph typically includes the number of edges, triples or triangles, mutual ties, and a range of k-stars of different values. In addition to these two parameterizations, contemporary ERGM models offer a wide variety of possible attributes that can be selected based on the underlying assumptions of dependence within the network being modeled.
A typical objective in ERGM analysis is an empirical estimation of the model, which is an effective means by which to draw statistical inference from network data. When estimating an ERGM, the process begins with an observed network such as the network of trade flows between countries for a given year. An ERGM is specified given the assumed dependencies within the model. The objective is to estimate parameter values of the ERGM such that the observed network is the maximally likely network to have formed given the distribution of all possible networks. The estimated parameters provide information as to the relative importance of each attribute in the observed network and indicate the types of network relationships that are important.
In what follows, the estimation procedures described will be limited to unweighted networks. Similar work on weighted networks is arising in the literature (see, for example, Krivitsky (2012) and Desmarais and Cranmer (2012)), but is still considerably less developed than the literature and procedures for unweighted networks.
Estimation of the parameters is essentially a maximum likelihood problem. The desired estimates are those that make the observed network the most likely to be observed. One method of estimating these parameters is to use standard maximum likelihood techniques on equation (4). However, doing so requires the computation of the normalizing coefficient which is contingent on the sample space consisting of all possible networks. This poses a computational problem for even relatively small networks where the magnitude of the set of all possible networks is for directed networks or for undirected networks. As such, standard maximum likelihood approaches are infeasible for even modestly sized networks.
As an alternative, Strauss and Ikeda (1990) and Wasserman and Pattison (1996) describe a modified approach that utilizes a maximum pseudo-likelihood technique. The original ERGM specification given by equation (4) can be reformulated as a logit model in terms of individual link formation. If denotes the complement of link (that is, the set of all other links excluding ), denotes the network with the addition of link , and denotes the network with link removed, then a logit function for the ERGM can be written
| (5) |
The logit function models the log odds of individual link formation contingent on the rest of the network. By doing so, the normalizing coefficient is eliminated from the model making computation easier. Estimation of the logit function using maximum psuedo-likelihood techniques requires the computation of the change statistic , which describes how each attribute changes as a specific link is added or removed from the network, but is generally feasible. However, while maximum pseudo-likelihood estimation of this logit function has the advantage of being readily computed using standard statistical tools, it suffers from a general concern that its estimation results in biased estimates and potentially poor approximations of the standard errors (see Robins et al. (2007) and Snijders (2002)). For these reasons, maximum pseudo-likelihood estimation has largely been replaced by Monte Carlo estimation methods based on (5).
Most recent work on ERGM estimation has utilized Markov Chain Monte Carlo (MCMC) maximum likelihood estimation. A brief summary of this process will be included here but Snijders (2002) and Lusher et al. (2013) provide more detailed descriptions of the methodology. On a basic level, MCMC techniques are used in order to generate a sampling distribution of networks that can then be used for statistical inference. Parameter values are proposed and the MCMC process generates a chain of network realizations with the hope that the sequence of networks converges to a distribution of networks such that the observed network is centered within the distribution and represents the most likely network that could have formed.
The process begins with the selection of initial parameter values .4 Next, an arbitrary network is initialized as a starting point for the simulation process. A sequence of networks is generated through a stochastic process in which a single link is selected at random at each step along the sequence. The current network is altered with respect to this one link such that the link is added if or removed if , resulting in a new proposed network . The two potential ensuing networks and are compared and the alteration to is accepted if the resulting network is sufficiently likely to occur given the previous network. This process typically employs a Metropolis-Hastings algorithm in which the proposed network is evaluated according to a Hastings ratio such that the proposed network is accepted with probability
The Metropolis Hastings algorithm accepts the proposed network if it is more likely than the previous network or–if it is less likely than the status quo network–with some probability that is decreasing in the likelihood ratio. The Hastings ratio can be generated using essentially the same logit model as described above in equation (5) and is based on the initial parameter values and the resulting change statistics.
This Markov process governed by the Metropolis Hastings algorithm generates a sequence of -many networks with the intention of creating a sampling distribution. This Monte Carlo procedure typically includes a burn-in period following the initialization of the starting network that omits the first -many networks generated so as to eliminate any memory of the starting network. By generating the sampling distribution one link at a time, significant autocorrelation tends to arise between subsequent networks in the sequence. To mitigate this autocorrelation, MCMC procedures typically use thinning methods that only include every th network in the sampling distribution. All other networks contained within the interval of -many networks are excluded. Thus, the ultimate sampling distribution consists of the the networks so that there is limitted autocorrelation within the sequence.
Following the Monte Carlo simulation process, the resulting sample of networks is compared to the observed network in order to determine if the model and initial parameter values are a good fit. If the estimation was successful, the distribution of sample networks ought to have attribute distributions centered around the attributes present in the observed network. If this holds, the parameter values are those that make the observed network the most likely network that could have formed, thereby solving the underlying maximum likelihood problem. If, however, the sampling distribution is not acceptably centered around the observed network, alterations are made to the initial parameter values and the process is repeated in subsequent iterations using updated sets of parameter values , until a satisfactory set of parameter values is found. Once an accurate set of parameter values is identified, the goodness-of-fit is tested by simulating a collection of additional networks using the estimated parameters and checking that they are suitably replicating the desired features of the observed network. The model and estimated parameter values are said to fit well if the networks from the simulated sample share the same characteristics on average as the observed network. For example, the average number of links or the distribution of -stars are similar.
If these diagnostic tests are satisfied, the final parameter estimates may be accepted and the estimation procedure is concluded. The estimates can then be used to describe dyadic dependencies within the model. The estimates themselves can be interpreted in terms of log odds as in equation (5). The log odds of a link forming depends on its relative position in the network. Suppose, for example, that by forming link , the link represents an additional link, a mutual tie, and completes a cyclical triple. The log-odds of that link forming would be equal to . In general, the sign and magnitude of each coefficient can be used to describe the relative importance of each modeled attribute and respective dependency. Positive estimates identify the network relationships that are likely to inspire link formation while negative coefficients describe those that tend to prevent link formation. The magnitude of the estimates further specifies the strength of these dependencies. Thus, using this information, a more complete understanding of the interrelationships in the network can be attained.
Before proceeding to the next section and the ERGM analysis of international trade flows, some time ought to be spent describing the methods by which ERGMs are estimated in practice. In recent years, several popular software packages have emerged that facilitate the estimation of a wide range of ERGM specifications. Two of the most popular are statnet5 and Pnet6. The work provided in the remainder of this paper utilizes the statnet software.
The statnet suite (Handcock et al., 2003) is a package containing a variety of tools to facilitate the analysis of networks and is used within the open-source software R. In addition to providing powerful ERGM estimation procedures, it also includes tools to perform other network oriented tasks such as graphing procedures and the generation of network descriptors. For additional information on the use of statnet, see Goodreau et al. (2008) and Handcock et al. (2008).
In order to study the properties of the international trade network and further identify higher-level dependencies, I estimate ERGMs using bilateral trade data for several years. The data originates from two sources. The first source is the BACI data set made available by Gaulier and Zignago (2010), which provides bilateral trade flows.7 The second data source is a gravity data set made available by Gurevich et al. (2017), which is an extension up to year 2016 of the data set made available by CEPII.8 The compiled data set consists of bilateral trade flows, GDP figures for both importing and exporting countries, a measure of population weighted distance, and indicators for common language, contiguity, and joint membership in a regional trade agreement.9
ERGM estimates were constructed for two networks: the 1995 and 2004 world trade networks. Both networks were modeled according to the following specification.
Under this specification, the world trade network is assumed to be dependent on the topological features and links as well as the social selection attributes , , , , and . The topological attributes condition the estimation on matching the expected number of trading relationships present in the network and the number of reciprocal relationships. Ideally, the set of topological attributes would contain more types of higher level dependencies than the two presented here. However, computational feasibility represents a significant limitation with current estimation procedures. The selected set of two attributes is the only set for which the estimation converges within a reasonable period of time.10 The social selection attributes were selected to mirror a standard specification of gravity models. In the case of GDP, the estimation seeks to match the covariance present between the nodes in the network with respect to their GDPs. If nodes with similar GDPs trade at a higher frequency in the observed trade networks, then this attribute ought to exhibit a positive coefficient in the above model. The remaining attributes assume that the world trade network is dependent on a series of other networks entirely. Distance, common language, contiguity, and RTAs each represent secondary networks composed of the same countries. For example, Figures 3 and 4 each depict these secondary networks for common language and contiguity. The model assumes that the world trade network (Figure 2) is dependent on these secondary networks such that each coefficient reflects the covariance between a link in the trade network between two nodes and the presence or absence of a corresponding link in the secondary network. Taken together, the model is quite similar to a standard gravity estimation. However, the underlying network approach makes it possible to identify higher level dependencies that are not ordinarily identified in a gravity framework.
The results of the estimation procedure are presented in table 5. Broadly speaking, the results largely support the claim that higher level dependencies exist within the world trade network. The structure of the trade network as well as the secondary networks and node characteristics to which it is compared are highly significant in explaining the formation of trade links. The ERGM based results here are largely in line with the probit results presented earlier in section 2, providing evidence that these dependencies are robust.
Looking more closely at the individual estimates, we can better characterize the dependencies underlying the formation of the world trade network. Recall that the estimates for each attribute reflect the marginal contribution to the log odds of link formation with the sign on each coefficient indicating whether it increases or decreases the likelihood of trade formation. The attribute establishes a baseline likelihood of forming a link and is similar to the constant in a standard regression. The coefficient is positive, implying that a country importing from another country is more likely if they are exporting to that country. The GDP coefficient is positive as well, implying that countries with larger GDPs tend to trade with each other with a higher likelihood. The relatively small magnitude of the estimate itself is simply a result of the scaling of the variable. Link formation is negatively correlated with the network of distances, as would be expected; each additional 1000 miles reduces the log odds of trade by about 0.07. Curiously, the trade network is negatively correlated with the common language network on average with trade less likely if both countries speak the same language. Contiguity and regional trade agreements are both positively correlated and each increase the likelihood of trade formation, which is consistent with most prior research.
| 1995 Network | 2004 Network | |
| Density: 0.416 | Density: 0.565 | |
| (1) | (2) | |
| edges | 1.584 | 0.863 |
| (0.0004) | (0.0004) | |
| mutual | 3.022 | 2.322 |
| (0.0004) | (0.0004) | |
| GDP | 3.528e-6 | 4.065e-6 |
| (0.069e-6) | (0.084e-6) | |
| Distance Network | 6.993e-5 | 7.507e-5 |
| (0.116e-5) | (0.112e-5) | |
| Language Network | 0.067 | 0.075 |
| (0.001) | (0.0005) | |
| Contiguous Network | 0.394 | 0.483 |
| (0.002) | (0.003) | |
| RTA Network | 0.585 | 1.479 |
| Akaike Inf. Crit. | 38,309.660 | 39,781.250 |
| Bayesian Inf. Crit. | 38,370.280 | 39,841.870 |
Note: p0.1; p0.05; p0.01
The estimated log likelihoods can also be converted to probabilities of trade formation.11 In 1995, the log odds of a county importing from another country if they share a border, are 500 miles apart, and the new link would complete a reciprocal relationship is . These odds imply a probability of link formation of about 0.86. Thus, it is clear that such conditions are highly conducive to the formation of trading relationships. To demonstrate the relative importance of reciprocity we can examine the effect of removing that characteristic. Were the link not mutual, the probability of formation would drop to only about 0.23. Thus it is clear that this higher level network dependency has a considerable influence on the formation of the international trade network in 1995.
Comparing trade in 1995 to 2004, we can observe several changes in the nature of the trade networks. Overall, the network has become much more dense overtime. In 1995, only about 42 percent of possible trade links were present in the network. By 2004, that percentage had increased to nearly 57 percent. As such, the coefficient for the edges attribute has grown over time, implying that the likelihood of link formation has grown absent other relevant attributes. The relative effect of reciprocal relationships has declined slightly in that time period, suggesting that mutual trade has become less important. The remaining attributes have all increased in magnitude between 1995 and 2004. This suggests that even though links have become more likely in general, their covariance with other relationships has increased as well. The links that are still absent from the network are those which share the weakest relationships to the node attributes and secondary networks. Thus, secondary network connections have become increasingly influential between 1995 and 2004.
Ultimately, these results provide compelling evidence that the formation of trade relationships relies to a significant degree on the network relationships that countries have with one another, both directly and indirectly. In order to properly understand and account for the determinants of bilateral trade, these higher level dependencies ought to be considered explicitly in models of trade. Leaving them to multilateral resistances and fixed effects overlooks a tremendous amount of potential information about the way countries trade. Despite facing computational limitations, ERGM analysis in particular represents a promising methodology for the continued research of higher level dependencies and multilateral resistance.
The role of network dependencies in international trade represents an important direction for understanding the determinants of trade flows. Prior research has consistently indicated that the trade between two countries is influenced by a wide variety of relationships that these countries share not only with each other but with all other countries. While most traditional trade research has overlooked these higher level dependencies, recent advances in empirical trade and network analysis are beginning to allow for the inclusion of these significant trade determinants. This paper describes two such method using gravity and random exponential graph modeling techniques.
By viewing international trade as a network formation problem that is dependent on underlying characteristics of the network, statistical inference is possible. The series of probit and ERGM estimations using bilateral trade data described in prior sections provide strong evidence that higher level network dependencies are present in international trade data. The ways in which countries trade with one another affects the specific decision to trade with any particular country. Countries have a strong proclivity for trading with one another in a mutual way and correlate to an increasing degree with the other ways in which they are networked, such as language, borders, and RTAs. These results are generally consistent with prior research and provide new insight into the influence of network relationships on international trade.
The work presented here using ERGM methods utilizes what appears to be a previously unused technique in the area of international trade. While ERGM analysis is not unique with respect to its ability to evaluate higher level network effects, it does offer several advantages over alternative methodologies due to its considerable flexibility with respect to the types of assumed dependencies that can be included in a model. Despite current limitations with estimation procedures, future research using ERGMs appears promising. In particular, the estimations using less dense, sector level trade networks appear to be less susceptible to common estimation difficulties and could be an interesting area to study more heavily. At the disaggregated level, the tendency to trade with nearly all potential partners becomes less significant, allowing for more effective inference about the underlying network effects. In these cases, the the decision concerning with whom a particular country decides to trade a particular product is likely a more nuanced question and will exhibit greater dependencies on trade networks. Further, ERGM analysis provides a potentially powerful tool for analyzing global supply chains where the patterns of trade and the localization of production stages is of the utmost interest.
Anderson, J. E. and E. van Wincoop (2003). Gravity with Gravitas: A Solution to the Border Problem. American Economic Review 93, 170–192.
Berthelon, M. and C. Freund (2008). On the conservation of distance in international trade. Journal of International Economics 75(2), 310–320.
Brun, J.-F., C. Carrère, P. Guillaumont, and J. de Melo (2005). Has Distance Died? Evidence from a Panel Gravity Model. The World Bank Economic Review 19(1), 99–120.
Chaney, T. (2014). The Network Structure of International Trade. The American Economic Review 104(11), 3600–3634.
De Benedictis, L., S. Nenci, G. Santoni, L. Tajoli, and C. Vicarelli (2013). Network Analysis of World Trade using the BACI-CEPII dataset. CEPII Working Paper 24.
De Benedictis, L. and L. Tajoli (2011). The World Trade Network. World Economy 34(8), 1417–1454.
Deguchi, T., K. Takahashi, H. Takayasu, and M. Takayasu (2014). Hubs and authorities in the world trade network using a weighted HITS algorithm. PLoS ONE 9(7).
Desmarais, B. A. and S. J. Cranmer (2012). Statistical inference for valued-edge networks: The generalized exponential random graph model. PLoS ONE 7(1).
Dueñas, M. and G. Fagiolo (2013). Modeling the International-Trade Network: A gravity approach. Journal of Economic Interaction and Coordination 8(1), 155–178.
Felbermayr, G. J. and F. Toubal (2010). Cultural proximity and trade. European Economic Review 54, 279–293.
Fontagné, L., C. Mitaritonna, and J. E. Signoret (2016). Estimated Tariff Equivalents of Services NTMs.
Frank, O. and D. Strauss (1986). Markov Graphs. Journal of the American Statistical Association 81(395), 832–842.
Gaulier, G. and S. Zignago (2010). BACI: International trade database at the product-level (the 1994-2007 version).
Goodreau, S. M., M. S. Handcock, D. R. Hunter, C. T. Butts, and M. Morris (2008). A statnet Tutorial. Journal of statistical software 24(9), 1–27.
Gurevich, T., P. Herman, S. Shikher, and R. Ubee (2017). Extending the CEPII Gravity Data Set.
Handcock, M. S., D. R. Hunter, C. T. Butts, S. M. Goodreau, and M. Morris (2003). statnet: Software tools for the Statistical Modeling of Network Data.
Handcock, M. S., D. R. Hunter, C. T. Butts, S. M. Goodreau, and M. Morris (2008). statnet: Software Tools for the Representation, Visualization, Analysis and Simulation of Network Data. Journal of Statistical Software 24(1), 1–11.
Head, K., T. Mayer, and J. Ries (2010). The erosion of colonial trade linkages after independence. Journal of International Economics 81(1), 1–14.
Helpman, E., M. Melitz, and Y. Rubinstein (2008). Estimating Trdae Flows: Trading Partners and Trading Volumes. The Quarterly Journal of Economics 123(2), 441–487.
Hoff, P. D. (2005). Bilinear Mixed-Effects Models for Dyadic Data. Journal of the American Statistical Association 100(469), 286–295.
Hofstede, G. (1980). Cultures Consequences: international differences in work-related values. Beverly Hills, CA: Sage Publications.
Hutchinson, W. K. (2005). ”Linguistic Distance” as a Determinant of Bilateral Trade. Southern Economic Journal 72, 1–15.
Krivitsky, P. N. (2012). Exponential-family Random Graph Models for Valued Networks. Electronic Journa of Statistics 6, 1100–1128.
Ku, H. and A. Zussman (2010). Lingua Franca: The Role of English in International Trade. Journal of Economic Behavoir & Organization 75, 250–260.
Linders, G.-j. M., A. Slangen, H. L. de Groot, and S. Beugelsdijk (2005). Cultural and Institutional Determinants of Bilateral Trade Flows. Tinbergen Institute Discussion Paper.
Lusher, D., J. Koskinen, and G. Robins (2013). Exponential Random Graph Modles for Social Networks: Theory, Methods, and Applications. Cambridge University Press.
Melitz, J. (2008). Language and foreign trade. European Economic Review 52, 667–699.
Rauch, J. E. (1999). Networks versus markets in international trade. Journal of International Economics 48(1), 7–35.
Rauch, J. E. and V. Trindade (2002). Ethnic Chinese networks in international trade. The Review of Economics and Statistics 84(1), 116–130.
Robins, G., P. Pattison, Y. Kalish, and D. Lusher (2007). An introduction to exponential random graph (p *) models for social networks. Social Networks 29(2), 173–191.
Snijders, T. A. (2002). Markov Chain Monte Carlo Estimation of Exponential Random Graph Models. Journal of Social Structure 3(2), 1–5.
Strauss, D. and M. Ikeda (1990). Pseudolikelihood Estimation for Social Networks. Journal of the American Statistical Association 85(409), 204–212.
Ward, M. D., J. S. Ahlquist, and A. Rozenas (2013). Gravity’s Rainbow: A dynamic latent space model for the world trade network. Network Science 1(01), 95–118.
Wasserman, S. and P. Pattison (1996). Logit models and logistic regressions for social networks: I. An introduction to Markov graphs and p*. Psychometrika 61(3), 401–425.
1Page-Rank is the method famously used by Google to sort internet search results.
2In the case of a directed network, -stars may be specified as either in--stars or out--stars in order to identify the direction of the relationship.
3A triangle describes a complete undirected relationship between three nodes or a directed relationship between three nodes in at least one pattern. Three node directed relationships can follow two possible patterns: transitive triples (, , ) or cyclical triples (, , ).
4There are several common methods used for this selection employed by ERGM statistical packages. Two frequently used methods are the Geyer-Thompson approach (used by statnet and in the analysis in the following section) and the Robbins-Monro algorithm (see Lusher et al. (2013), p149-154).
6http://www.swinburne.edu.au/fbl/research/transformative-innovation/our-research/MelNet-social-network-group/
7Available for download at http://www.cepii.fr/cepii/en/bdd_modele/bdd.asp
8The extension is available for download at https://www.usitc.gov/research_and_analysis/staff_products.htm
9Common language is defined here as having at least 9% of the population in both countries speak the same language.
10Inclusion of attributes such as triangles, star distributions, or degree distributions has resulted in estimations that run for days on end, improve by marginal amounts with each iteration, but never manage to converge. Hopefully, continued improvements to these estimation procedures will rectify this limitation.
11If the log odds of a link forming is , the probability of formation is .