Model Details
In this report, the markets in Washington State for individually quick frozen (IQF) and non-IQF[1] raspberries, either processed or intended for processing, are analyzed using separate partial equilibrium models. The models assume that the prices in the IQF market have no bearing on the non-IQF market and vice versa. This is consistent with the limited substitutability between IQF and non-IQF raspberries, and the fresh raspberries used to produce each, as evidenced by the distinct market channels for the two product categories described in chapter 3. Buyers' preferences in each market are modeled by demand in which there is a constant elasticity of substitution between the domestic and imported products.[2] The two models account for supply of raspberries from two sources, Washington and imports. Consumers in the models do not differentiate between raspberries from different countries of import, which would have limited impact on the domestic results.[3] The model estimates the elasticity of substitution between Washington raspberries and imports based on the elasticity of substitution from different source countries using trade data and an econometric model. The model is then calibrated to the market shares of Washington raspberries and imports in order to capture the extent of substitution between these sources.
In the model markets for both product categories, the quantity of imports is treated as exogenous to the model, meaning that changes in the price of imports (an output of the model) do not change the quantities of imports (treated as an input to the model).
The Washington marginal cost curve in the IQF market is upward sloping, reflecting capacity constraints stemming from limited availability of freezing tunnels and specialized equipment.[4] As discussed in chapter 3, five to six processors account for three-fourths of Washington production. Because of the high cost of the equipment, most small processors do not have IQF capacity. As a result, these few processors may have an even higher market share in IQF production and likely have some price setting power. Given these market features, information from industry representatives, and limited availability of data, the Washington IQF sector of the market is modeled using a monopoly pricing structure as an approximation of the market. The Washington industry for non-IQF raspberries is less concentrated, with more growers and processors than the IQF sector. Washington supply of non-IQF raspberries is modeled as perfectly competitive and with a constant elasticity of supply. While available acreage would also limit the maximum capacity for non-IQF raspberry product, that constraint is assumed not to bind in the model estimation or simulation and is not modeled allowing production to change significantly in response to changes in market prices.[5]
For each product category, the model is calibrated to annual data from 2010 to 2020.[6] The model is then used to simulate a counterfactual scenario by reducing the quantity of imports for that product category. The amount of reduction to imports in the counterfactual is based on observed features of the growth rates of imports in each market, further described below. In both counterfactual model scenarios, prices for both domestic and imported raspberries and production for domestic raspberries adjust to a new equilibrium level.
Model Equations
In the following equations, subscripts 
and 
are used to denote product-specific and source-specific variables. The 
subscript denotes the domestic source and the 
subscript denotes the foreign (imported) source. The total demand shifter for product 
is 
, and the weight for source 
for product is 
. The price elasticity of total demand for product is denoted as 
and the elasticity of substitution between sources of product is denoted as 
. Given the prices for each source of product , the quantity demanded for product from source is given below.
The price index 
is given by the following equation.
The two models use different forms for domestic supply functions. The IQF market has an asymptotic supply function representing the capacity constraints present in that market. The non-IQF market has a constant elasticity of substitution supply function.
In the IQF supply function, 
is the maximum capacity for quantity, and 
is a parameter that determines the curvature of the asymptotic function. In the non-IQF supply function, 
is a supply shifter and 
is the price elasticity of supply.
The quantity of imports is treated as exogenous in both models, so the supply functions for imports are given trivially by 
where 
is the fixed level of quantity imported of product from the foreign source.
In the IQF market, the equilibrium is defined by a pair of prices 
and 
such that (1) the marginal revenue of the Washington good equals the marginal cost of production of the Washington good and (2) the quantity demanded of the foreign good equals the quantity supplied of the foreign good.[7] In the non-IQF market, the perfectly competitive equilibrium is defined by a pair of prices 
and 
such that (1) the quantity demanded of the Washington good is equal to the quantity supplied of the Washington good and (2) the quantity demanded of the foreign good equals the quantity supplied of the foreign good.
Estimation and Calibration
Constant and annual parameters are show in tables F.1 and F.2. The demand parameters are estimated directly from the market data for the Washington industry. Some elasticity parameters could not be precisely estimated with the available data, so unit elastic parameters are used.[8] The unit elasticity assumption is applied to the total price elasticity of demand for both markets, implying that overall expenditure (price times quantity) in a year does not change with price. While this assumption is common in similar models and has been found to hold for many products, analysis elsewhere in this report suggests that buyers may switch to other fruits if raspberry prices rise. However, data to estimate these parameters were unavailable and the use of unit elastic parameters was unlikely to substantially alter the results. The demand elasticities of substitution are estimated through trade costs following the econometric methodology described in Riker 2020.[9] Prices are normalized to 1 and the demand weights for Washington and imported raspberries are calculated from their respective shares of total expenditure in each market. The domestic data cover only processed raspberries (e.g., IQF, bulk frozen, puree, juice, etc.) from Washington, while the import data encompass both processed raspberries and fresh raspberries intended for processing. In the absence of end-use data for imports, including the fresh raspberries for processing in the non-IQF aggregation provides the best approximation of the competition that Washington producers and processors face.[10] The preference weights calculated for the demand function implicitly take into account the differences in quality (in this case, stemming from some imports being less processed) between Washington and imported sources. The total price elasticity of demand is assumed to be −1 in both industries, effectively holding total expenditure on each category fixed while allowing the share of expenditure on domestic or imported products to change.
The marginal cost functions each have one parameter with a selected value and one parameter that is calibrated in the model. For the asymptotic marginal cost function in the IQF market, the maximum possible quantity in each year was set at 10 percent past the actual quantity produced in Washington.[11] The curvature of the asymptotic marginal cost function was calibrated so that the equilibrium production in the model matched the actual production given the selected capacity constraint. In the non-IQF market, the constant price elasticity of supply was set to a standard value of 1.0 given data limitations preventing estimating this parameter. This assumption means that percentage changes in the quantity supplied are exactly equal to percentage changes in price. The supply shift parameter was calibrated so that the equilibrium production in the model matched the actual production, given the selected supply elasticity.
Table F.1 Constant parameters
| Parameter | Symbol | Value | Method |
| IQF Total elasticity of demand |
| −1 | Chosen—common value |
| Non-IQF total elasticity of demand |
| −1 | Chosen—common value |
| Non-IQF elasticity of supply |
| 1 | Chosen—common value |
| IQF elasticity of substitution |
| 4.7 | Econometric estimate |
| Non-IQF elasticity of substitution |
| 8.5 | Econometric estimate |
| IQF normalized price |
| 1 | Numeraire |
| Non-IQF normalized price |
| 1 | Numeraire |
Source: USITC staff.
Table F.2 Annual parameters
| Parameter | Symbol | Method |
| IQF supply function curvature |
| Calibrated to match observed quantity given normalized price |
| Non-IQF supply shifter |
| Calibrated to match observed quantity given normalized price |
| IQF demand shifters |
| Matched ratio of Washington to imported sales |
| Non-IQF demand shifters |
| Matched ratio of Washington to imported sales |
| IQF import quantity |
| IQF imported customs value given normalized price |
| Non-IQF import quantity |
| Non-IQF imported customs value given normalized price |
| IQF capacity constraint |
| Observed quantity multiplied by 1.1 (see explanation in text) |
Source: Model calibration performed by USITC staff from multiple data sources.
Counterfactual Scenarios
The counterfactual scenarios do not correspond to any analysis of specific policy alternatives. Instead, they were chosen based on aggregate import trends. The country profiles in chapters 4–7 discuss the country-specific factors that impacted the overall U.S. import trade trends.
Both scenarios involve identifying a marked increase or surge in the value of imports and then reducing the growth rate of imports in the identified surge years to simulate growth rates in the years outside of the surge. A surge here refers to a short number of years with growth rates that are significantly higher than the average growth rate in the period overall. For the counterfactual scenario, the difference between the average surge growth rate and the average non-surge growth rate is subtracted from the growth rate in each surge year. The simulation then creates a counterfactual level of imports for each year from the beginning of the surge to 2020 based on the import volume of the prior year and the new counterfactual growth rate in the surge years, or actual growth rate in the non-surge years, for each year in IQF and non-IQF imports. This brings the average growth rate of the 11-year period down to the average non-surge growth rate while still allowing variation between years.
In the IQF scenario, raspberry imports saw a sharp surge in imports from 2013–14, but then declined to levels comparable to 2010 and 2012 before increasing again in 2020. The average growth rate in the surge years is 40.8 percent, compared to −2.3 percent for non-surge years. When the surge is removed, the counterfactual models a decline in the value of IQF imports in the later years of the period from levels seen in 2010–12. Figure F.1 shows the actual and counterfactual percentage change in value of IQF imports and value of IQF imports.
Figure F.1 Actual and counterfactual percentage changes and levels for gross sales of imported IQF raspberries, 2010–20
In percent change over previous year and millions of U.S. dollars. Underlying data for this figure can be found in appendix H table H.33.
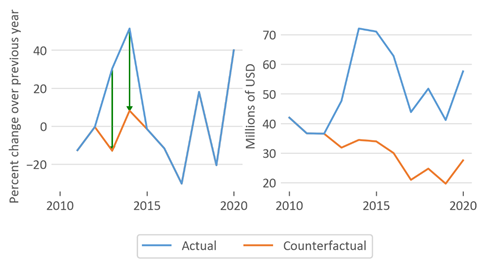
Source: USITC DataWeb/Census, accessed March 19, 2021 and calculations by USITC.
In the non-IQF scenario raspberry imports saw a sharp increase in value between 2012 and 2015 and then remained elevated as compared to 2010 and 2011.[12] The average growth rate in the surge years is 35.9 percent, compared to 1.7 percent for non-surge years. When the surge years are excluded, the value of sales of the Washington non-IQF processed raspberries stayed comparatively flat over the same period. Figure F.2 shows the actual and counterfactual percentage change in value of non-IQF imports and value of non-IQF imports.
Figure F.2 Actual and counterfactual percentage changes and levels for gross sales of imported non-IQF raspberries, 2010–20
In percentage change over previous year and millions of U.S. dollars. Underlying data for this figure can be found in appendix H, table H.34.
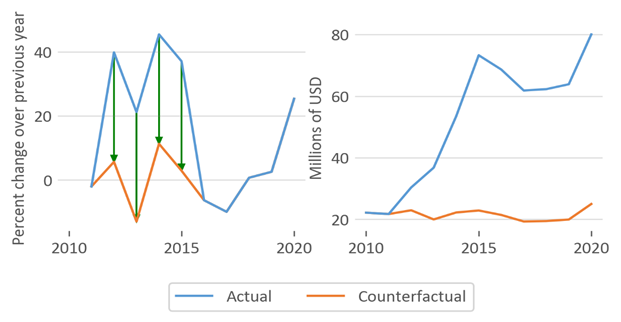
Source: USITC DataWeb/Census, accessed March 19, 2021, and calculations by USITC.
Limitations
The model only includes Washington production for the domestic market. While California and some other states produce some raspberries for processing, data limitations for the U.S. industry required restricting analysis to Washington State. Throughout chapter 9 and this appendix, domestic prices and production refer specifically to Washington producers unless stated otherwise. Market share results present Washington's share of the sum of sales value for Washington state and imported raspberries for processing, so the sales value of raspberries for processing of other states is not included.
The data for Washington and imported raspberries for processing and processed raspberries are not directly comparable. The Washington data are aggregated to broad categories, while the import data correspond to 10-digit statistical reporting numbers in the Harmonized Tariff Schedule of the United States (HTS). These statistical reporting numbers needed to be allocated into IQF and non-IQF raspberries, but many of the HTS numbers are not sufficiently broken out by product to precisely sort into these categories. Commission staff used product and country information to approximate what share of the data for each 10-digit statistical reporting number should be allocated to IQF and non-IQF, with a particular focus placed on the products with the most overall import value. These approximations also affect the estimated elasticities of substitution between Washington and imported raspberries for processing, since the methodology uses trade costs to estimate the elasticities. The HTS number sorting uses the same percentage allocations for the trade values and trade costs, potentially biasing the elasticity estimates. More details on how the data were prepared for this analysis are found in appendix E.
In addition, the import data include fresh raspberries intended for processing along with processed raspberries, while Washington data include only IQF raspberries, B-grade raspberries, and raspberry juice (these are slightly more processed products than the fresh berries intended for processing).
The models use imports as an exogenous input rather than a model output. Due to how import quantities are constructed in the IQF and non-IQF simulation scenarios, this assumption has limited impacts on the results for both domestic markets, and it is therefore a reasonable assumption in both models. In addition, the assumption that imports are not sensitive to prices in the United States seems especially reasonable for the non-IQF market. Mexico is the largest source of these imports and is mainly responsible for the increase in these imports in recent years. As described in chapter 5, the changes in the supply of non-IQF raspberries from Mexico, especially fresh raspberries for processing, were largely driven by factors other than the price of raspberries for processing in the United States. This is also consistent with public hearing testimony and industry interviews that suggested that the increase in fresh raspberries for processing from Mexico is a side effect of changes in the market for raspberries for fresh consumption.
The quantitative analysis is carried out using a series of static single-year simulations, which leads to some limitations in the analysis that come from ignoring dynamic features in marginal cost functions. In the IQF model, the capacity constraints (stemming from specialized freezing equipment) are calibrated based on the actual production in each year, and do not account for the fact that additional investment would likely have occurred if prices were higher. In that case, production would likely change by more and prices would change by less compared to the static model results.
In the non-IQF model, domestic supply is allowed to increase without a set constraint. In reality, available acreage (and therefore maximum quantity) depends partially on acreage in previous years. In particular, this limits how much production would actually be able to increase from one year to the next. The large increases in simulated Washington production in the surge years would likely have been more modest, although prices would have risen more. The simulated increase in production in the most recent five years were not as sharp, so this limitation is unlikely to have a large impact on the non-IQF results for the years of interest.
Robustness Check with Distribution of Substitution Elasticities
The models were recalibrated using a range of alternative elasticities of substitution between domestic and imported products to assess the sensitivity of the model results to those parameters (table F.3). The distribution of results generated by the range of elasticities is used to display confidence intervals for some variables of interest, such as the price and production figures in the main text. For each model, a normal distribution of alternative elasticities was produced using the point estimates and standard errors from the econometric estimation of the elasticity parameter. The distribution was approximated by 101 points, with alternative models being calibrated and simulated at each point.
Table F.3 Means and standard deviations for elasticity of substitution distributions
| Product | Mean (point estimate) | Standard deviation (standard error) |
| IQF | 4.7 | 0.5 |
| Non-IQF | 8.1 | 0.9 |
Source: Econometric estimations by USITC.
The model simulations are not particularly sensitive to the elasticities within the distributions checked. Tables F.4 and F.5 display the 5th, 50th, and 95th percentiles for several model result variables. The 50th percentile results are the ones presented in chapter 9. Of all the simulations performed, 90 percent have model results that fall between the 5th and 95th percentile results presented here.
Table F.4 Summary of elasticity of substitution robustness check of model results for Washington gross sales 2016–20
In millions of U.S. dollars
| Product | Actual value of Washington gross sales | 5th percentile estimate: simulation value of Washington gross sales | 50th percentile estimate: simulation value of Washington gross sales | 95th percentile estimate: simulation value of Washington gross sales |
| IQF | 225.1 | 291.6 | 295.2 | 297.7 |
| Non-IQF | 205.5 | 368.9 | 373.3 | 376.4 |
| Total | 430.6 | 660.5 | 668.4 | 674.2 |
Source: Econometric estimations by USITC.
Note: This table displays the actual and simulation (counterfactual) gross sales values at the 5th, 50th, and 95th percentiles.
Table F.5 Summary of model results using elasticity of substitution robustness check for counterfactual Washington prices and production above actual values 2016–20
In percentage over actual. Values are rounded.
| Product | 5th percentile: price | 50th percentile: price | 95th percentile: price | 5th percentile: production | 50th percentile: production | 95th percentile: production |
| IQF | 28.1 | 29.4 | 30.4 | 1.1 | 1.3 | 1.4 |
| Non-IQF | 33.9 | 34.7 | 35.3 | 33.9 | 34.7 | 35.3 |
| Total | 30.9 | 32.0 | 32.7 | 16.6 | 17.1 | 17.6 |
Source: Econometric estimations by USITC.
Note: This table displays simulation results of how much higher prices and production would have been in the counterfactual scenario described in this appendix.